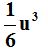Volumen de un tetraedro a partir del producto mixto de tres vectores.
Seguramente estudiaste la obtención del volumen del tetraedro a partir de su arista:
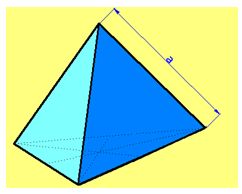
En la figura anterior tienes un tetraedro en el que el dato conocido es la arista (a) del mismo.
El volumen es:
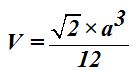
Sin embargo, podemos calcular el volumen de un tetraedro sirviéndonos del producto mixto de tres vectores.
Sabemos que la base de un tetraedro es un triángulo y si conocemos dos vectores podemos hallar su área tal a partir del módulo del vector producto de dos vectores como estudiamos últimamente:
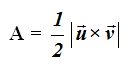
Para calcular el volumen de un sólido, la regla general es, área de la base por la altura, pero esto tiene unas limitaciones.
Cuando las figuras geométricas son prismas, cuerpos geométricos limitados por dos polígonos paralelos e iguales que son sus bases, y tantos rectángulos como lados tiene cada una de estas bases,la regla general anterior se cumple.
En el caso de las pirámides que son cuerpos geométricos cuyas bases son polígonos y sus caras triángulos, tantos como lados tiene el polígono de la base, has de tener en cuenta que, de un prisma triangular puedes obtener 3 pirámides de base triangular o tres tetraedros de igual volumen.
Esto quiere decir que el volumen de un prisma triangular equivale al volumen de TRES TETRAEDROS.
Por eso, el volumen de un tetraedro equivale a la tercera parte del volumen del prisma.
A continuación tienes una secuencia de figuras geométricas en la que puedes ver:
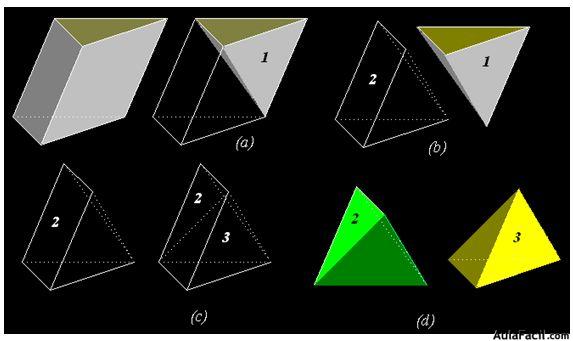
- Prisma triangular.
- En dos de las caras del prisma trazamos una diagonal y en (a)puedes apreciar la pirámide con el número 1.
- La figura geométrica (a) la hemos separado en dos partes tal como puedes ver en (b).
- La primera pirámide o tetraedro (en el caso de que todas las caras fuesen triángulos equiláteros ) está señalada con el 1 y el resto de la figura geométrica con el 2.
- Tomamos la figura correspondiente al número 2 y trazamos una diagonal en la cara que de cuatro lados (c). Señalamos con el 3 al resto de la figura.
- Separamos las figuras 2 y 3 (d) comprobando que son pirámides triangulares, y en el caso de que tuvieran caras formadas por triángulos equiláteros, serían tetraedros.
De aquí deducimos que el volumen de un tetraedro es igual a la tercera parte del volumen de un prisma regular triangular.
Pasemos a la práctica.
Tenemos un tetraedro cuyos vectores indicamos:
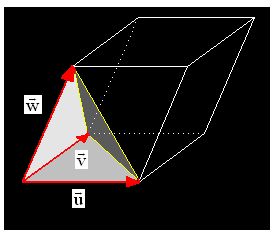
El volumen de este tetraedro tras lo estudiado hasta ahora teniendo en cuenta el producto mixto será:
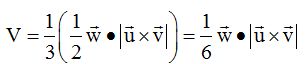
Aplicación:
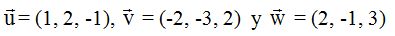
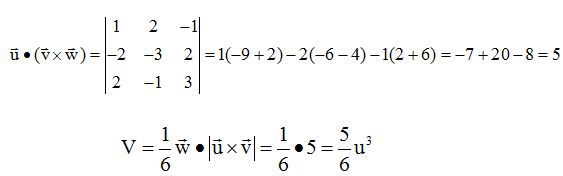
Respuesta: