Soluciones de Ejercícios

23.35  Sabes que la forma vectorial de la ecuación de una recta nos viene dada por las componentes de un punto P y las de un vector director .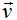

Si conocemos los puntos P  y Q  las componentes de 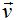 son: 

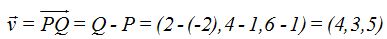
Siendo 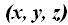 las componentes de un punto cualquiera podemos escribir en forma vectorial:

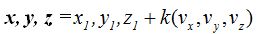
Sustituyendo valores:

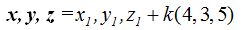
Calculamos el valor de cada componente:

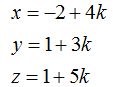
Esta disposición de los datos representan a la forma paramétrica.

23.36  Sirviéndonos de lo calculado en el ejercicio anterior tendemos despejamos el valor del parámetro k:

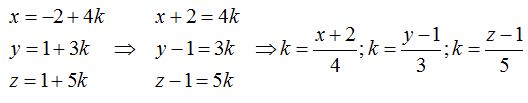
Dado que los valores de k han de ser iguales, escribiremos:

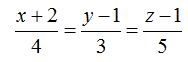
Esta es la ecuación de la recta en forma continua.

23.37  Ahora nos servimos de la ecuación en la forma continua del problema anterior y haciendo operaciones tendremos:

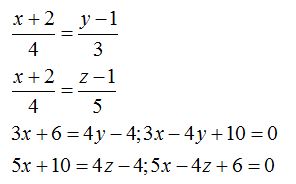
23.38   La ecuación general con los datos que disponemos la escribiremos:

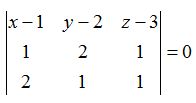
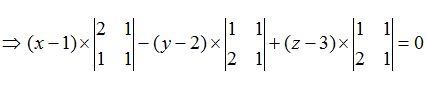
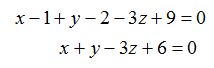
23.39  Es cierto que lo podríamos haber resuelto multiplicando los vectores 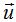y :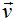

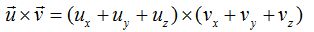
Si realizas el producto tendrás que tener en cuenta los signos  según “la ley del sacacorchos” que lo tienes explicado en la parte teórica dedicada a los: vectores en el espacio – producto vectorial de dos vectores referidos a la base canónica.

Dado que hacerlo de este modo como por el de la resolución del determinante al que hemos hecho referencia, éste, resulta mucho más sencillo y rápido, es por lo que lo hemos utilizado.

23.40  Calcula la ecuación de un plano que contiene el punto 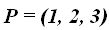 y el vector normal N =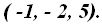 

Según el enunciado disponemos de tres datos:
1.- Un punto del plano.
2.- La normal.
3.- El producto de los dos vectores anteriores, por ser perpendiculares (sen 90º = 0)  nos da el valor cero.

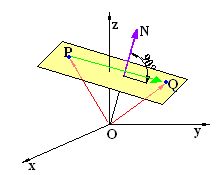
Siendo Q un punto cualquiera cuyas coordenadas son :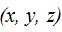

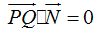
Esto quiere decir que: 

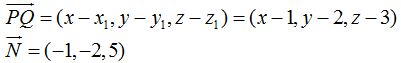
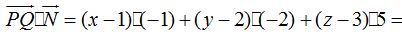
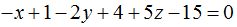
El resultado es: 

Comprobamos:

En la ecuación obtenida, sustituimos x, y, z por las coordenadas del punto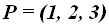 

y verificamos si el resultado es 0:

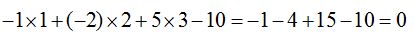
23.41  Sabemos que un punto cualquiera de la recta viene dado en la forma paramétrica, partiendo de la forma vectorial (puedo hacer uso de la forma que me resulte más cómoda):

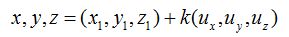
Escribo los valores que conozco:

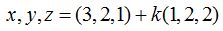
Forma Paramétrica:

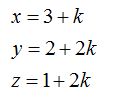
Compruebo si el punto 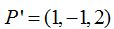 pertenece a la recta:

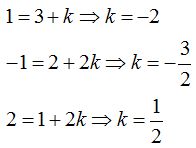
Para que el punto 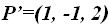 se halle en la recta, el valor de ktendría que valer lo mismo.

23.42  Como has visto en el problema anterior, para que un punto se halle en la recta, los valores de han de ser iguales y para que esto sea así:

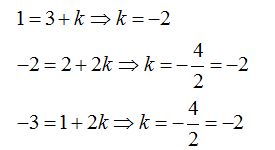
he modificado los primeros miembros de cada igualdad teniendo en cuenta que los valores de sean iguales, lo que me indica que el punto 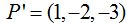 sí pertenece a la recta.

23.43    Compruebo si los puntos 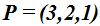y pertenecen a la misma recta haciendo uso de la forma continua de la ecuación de una recta en el espacio.

El vector director es .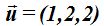

Lo compruebo de dos modos basándome en la forma continua de la ecuación de una recta en el espacio:

1) Las ecuaciones en la forma continua las escribo:

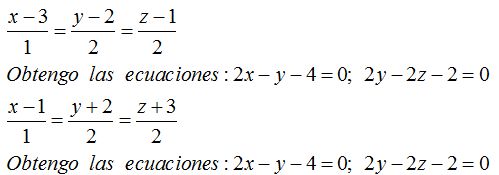
Puedes ver que he obtenido las mismas ecuaciones.

2) Otro modo de comprobación es, dada la primera ecuación en forma continua, sustituir en ella los valores de las componentes del segundo punto y ver si los cocientes son iguales:

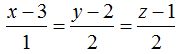
Sustituyo por los valores de las componentes del 2° punto:

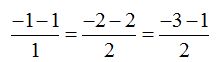
Obtengo cocientes iguales a 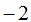.