Soluciones de Ejercícios
23.44 Los puntos son:
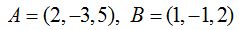y 
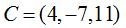
Calculo las componentes de los vectores: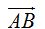 
y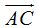 
:
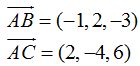
Para que los puntos estén alineados es preciso que el rango sea igual 1:
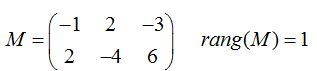
La segunda fila es dependiente de la 1ª (basta multiplicar por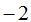 
a cada elemento de la 1ª para obtenerla).
23.45 Siendo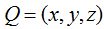 
un punto cualquiera del plano, el vector que une este punto con P vale:
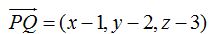
Como el producto de los vectores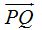 
y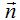 
por ser perpendiculares vale cero, podemos escribir:
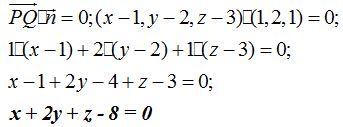
23.46 Conocemos, por los datos del problema, que la recta por ser perpendicular al plano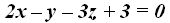 
su vector normal tiene como componentes: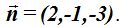 
Sabemos también, que la recta pasa por el punto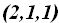 
, por lo tanto, será también el vector director de la recta, y su ecuación en la forma continua la podemos escribir:
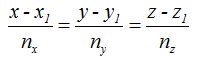
Sustituimos por los valores que conocemos:
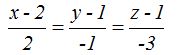
La recta queda determinada por estas dos respuestas:
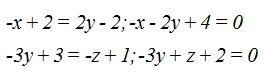
23.47 Primero dibujamos los elementos que intervienen en este problema.
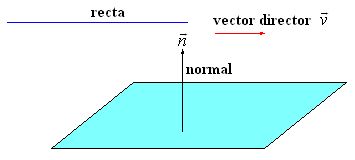
Sabemos que el producto escalar de dos vectores perpendiculares vale 0, es decir,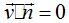 
.
(Como el producto nos tiene que dar un valor escalar - cero o un número distinto de cero, tendremos que calcular el producto escalar.
Otra cosa sería si tuviésemos que hallar, por ejemplo, los coeficientes de la ecuación de un plano, las componentes de una recta, etc., en estos casos tenemos que calcular el producto vectorial o producto cruz).
Conocemos las componentes del vector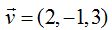 
que son los denominadores de las razones de la ecuación de la recta en la forma continua. El vector 
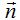por ser perpendicular al plano sus componentes son los mismos que los coeficientes del plano, es decir,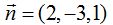 
Comprobamos si
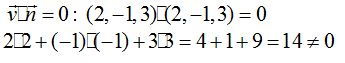
Vemos que no, esto quiere decir que la recta y el plano No son paralelos.
23.48 Conocemos las componentes del vector director (2,1,1).
Las componentes del vector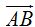 
:
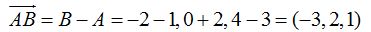
Recuerda que una ecuación del plano en su forma general es:
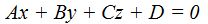
y las componentes de la normal son (A, B, C).
Podemos escribir:
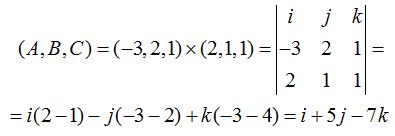
Vemos que las componentes de la normal son: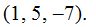 
Ahora podemos calcular la ecuación del plano ya que conocemos los valores de A, B y C: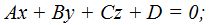 
sustituyendo valores tenemos: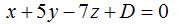 
Nos falta calcular el valor de D y para ello, dado que conocemos dos puntos del plano que son A y B los sustituimos por cualquiera de ellos.
Tomamos los valores de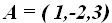 
y los sustituimos en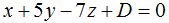 
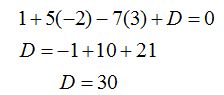
La ecuación del plano es: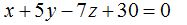 
23.49 Al sustituir por las componentes del punto B lo único que varía es el término independiente D, mientras que los coeficientes de las variables permanecen sin cambio. Al variar el valor de D, nos referimos a otro plano paralelo al anterior.
23.50 Primero comprobamos si los planos se cortan en una recta. Vemos que sí debido a que al ser linealmente independientes los
datos de las dos ecuaciones:
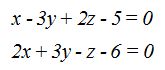
el rango de la matriz formada por los coeficientes y el de su ampliada valen 2, luego son secantes.
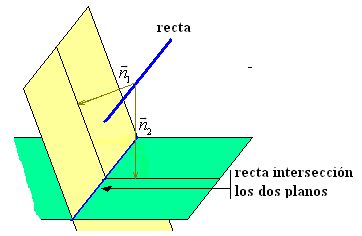
La recta de intersección de los dos planos es paralela a la recta en el espacio.
Las normales de un punto de la recta a cada plano son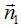 
y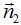 
.
Conocemos las ecuaciones de los planos en su forma general, lo que quiere decir que también conocemos las componentes de sus normales:
Al plano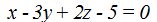 
le corresponde la normal 
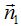cuyas componentes son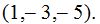 
Al plano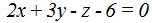 
le corresponde la normal 
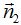cuyas componentes son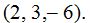 
Sabemos que el vector director de la recta lo podemos obtener por el producto vectorial de los vectores normales:
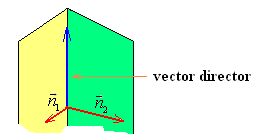
El valor del vector director de la recta nos vendrá dado por el producto vectorial de los vectores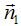 
y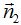 
.
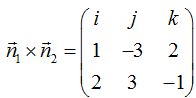
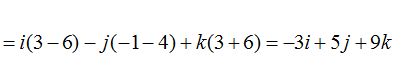
Recuerda que este método del cálculo del producto vectorial es más breve que hacerlo analíticamente.
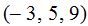de la forma continua.El problema nos dice que la recta pasa por el punto 
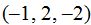, la ecuación escribiremos: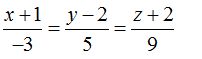
23.51 Del texto deduzco las componentes del vector director (denominadores de la forma continua):
.
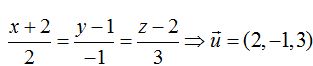Necesito conocer otro vector del plano y para ello dispongo de otro punto, llamemos B cuyas componentes las encuentro en los numeradores de la ecuación de la recta situada en el plano en la forma continua (cambiadas de signo):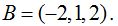 
Calculo el vector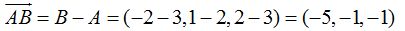 
Conocemos el vector que une el punto A con cualquier punto del plano Q cuyas componentes son x, y, z, luego, el vector :
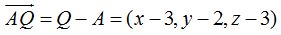
Tenemos los vectores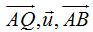 
y anteriormente dedujimos el determinante que nos sirve para resolver la ecuación implícita del plano cuando conocemos tres vectores en el plano:
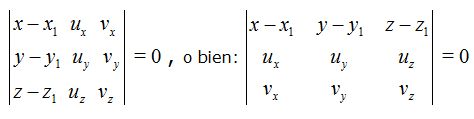
Sustituyendo valores:
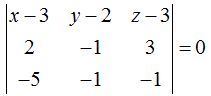
Resolvemos:
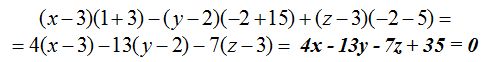
23.52 La normal de un plano que pasa por el punto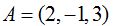 
es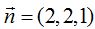 
¿cuál es su ecuación?
Con los datos que me ofrece el texto conozco los coeficientes de x, y, z de la ecuación del plano en su forma general y que corresponden a las componentes de la normal:
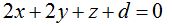
Añade el problema que uno de los puntos del plano tiene por componentes 2 ,– 1, 3.
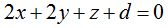para obtener el valor de d: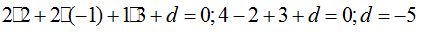
La ecuación es: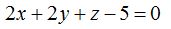 
23.53 La ecuación de un plano en la forma segmentaria vale, en este caso:
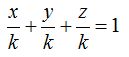
Haciendo operaciones:
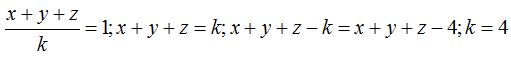
23.54 El producto vectorial de los vectores normales de las ecuaciones nos da el vector director. Las componentes de los vectores normales son, respectivamente:
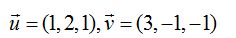
Vector Directo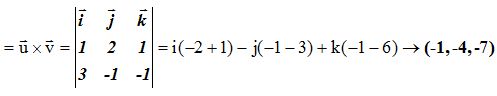 
23.55 Tomamos la matriz ampliada y a partir de ella efectuamos el cálculo del rango (en fondo amarillo la matriz de coeficientes):
