Desarrollo de Ejercícios
23.35 Una recta pasa por el punto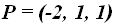 
y por el punto 
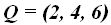escribe su ecuación en forma paramétrica.
Respuesta:
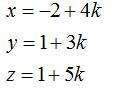
23.36 Escribe en forma continua la ecuación de la recta sirviéndote de los datos del ejercicio anterior.
Respuesta:
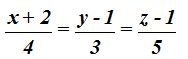
23.37 Sirviéndote de los datos anteriores, escribe ecuaciones de la recta en forma implícita.
Respuesta:
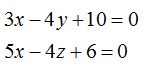
23.38 Escribe la ecuación de un plano que contiene el punto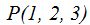 
y los vectores 
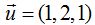y 
.
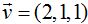Respuesta: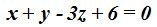 
23.39 El problema anterior está resuelto (en SOLUCIONES) por medio de un determinante. ¿No podríamos haberlo resuelto por el producto vectorial de dos vectores? ¿Por qué no lo hemos hecho así?
Respuesta: Sí. Porque resulta bastante laborioso.
23.40 Calcula la ecuación de un plano que contiene el punto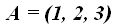 
y el vector normal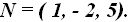 
Respuesta: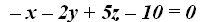 
23.41 Una recta que pasa por el punto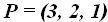 
es paralela al vector ¿podrías afirmar, aduciendo el porqué, con los datos anteriores, si el punto 
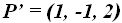pertenece a la misma recta?
Respuesta: El punto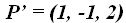 
no pertenece a la recta porque haciendo uso de la forma paramétrica, los valores que recibe el parámetro son diferentes en cada componente.
23.42 Basándote en el problema anterior, escribe un punto que sí se encuentre en la recta.
Respuesta: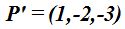 
23.43 Comprueba si los puntos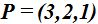 
y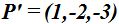 
de los dos últimos problemas pertenecen a la misma recta haciendo uso de la forma continua de la ecuación de una recta en el espacio.
Respuestas: Examina las soluciones.
23.44 Los puntos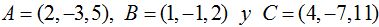 
¿pertenecen a la misma recta?
Nota.- Hazlo de un modo distinto a lo realizado en los dos últimos ejercicios.
Respuesta: Sí, porque el rango es igual a 1.
23.45 Halla la ecuación de un plano que pasa por el punto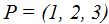 
y su vector normal es 
.
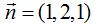Respuesta: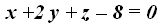 
23.46 Una recta pasa por el punto (2,1,1) y es perpendicular al plano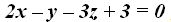 
¿Cuál es la ecuación de esta recta?
Respuestas:
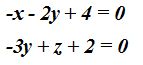
23.47 ¿Puedes asegurar que la recta
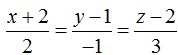es paralela al plano 
?
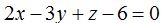Razona la respuesta.
Respuesta: La recta y el plano no son paralelos. El razonamiento en SOLUCIONES.
23.48 Los puntos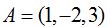 
y 
pertenecen a un plano y es paralelo a la recta:
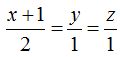¿cuál es la ecuación de dicho plano?
Respuesta: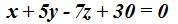 
23.49 Volvemos sobre el problema anterior y la pregunta es ¿Por qué da lo mismo, si hubiésemos sustituido, en el cálculo de la ecuación del plano por las componentes del punto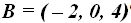 
?
Respuesta: Obtenemos un plano paralelo al anterior.
23.50 Una recta es paralela a los planos:
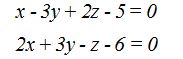y pasa por el punto 
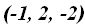escribe su ecuación en la forma continua.
Respuesta:
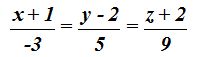
23.51 Halla la ecuación de un plano que pasa por el punto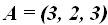 
y contiene a la recta de ecuación cuya forma continua es:
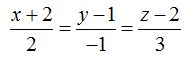
Respuesta: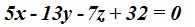 
23.52 La normal de un plano que pasa por el punto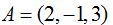 
es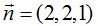 
¿cuál es su ecuación?
Respuesta: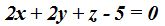 
23.53 Un plano corta a los ejes de coordenadas en los puntos situados a una distancia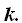 
del origen. ¿Cuánto ha de valer 
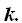para que el plano sea igual a 
?
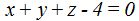Respuesta: 4
23.54 Si te dicen que la recta r viene dada del modo siguiente:
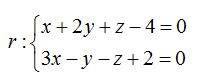¿Cuáles son las componentes del vector director?
Respuesta: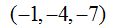 
23.55 ¿Cuál es la posición relativa de las rectas:
?
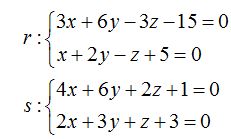Respuesta: Las rectas son paralelas.
