Posiciones Relativas de dos Planos. Rangos
¿Por qué hemos vuelto a estudiar el modo de calcular el rango de una matriz?
Porque podemos saber si dos planos son coincidentes, paralelos o secantes si conocemos el rango de la matriz formada por los coeficientes de las variables y el de la matriz ampliada.
Si el rango de la matriz de coeficientes y el de su ampliada son iguales a 2, los planos se cortan.
Si el rango de la matriz de coeficientes y el de su ampliada son iguales a 1, los planos son coincidentes.
Si el rango de la matriz de coeficientes es igual a 1 y el de su ampliada es igual a 2, los planos son paralelos.
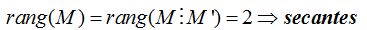
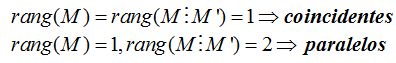
Resumiendo:
Las ecuaciones de dos planos son:
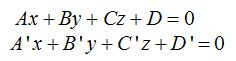
Llamando M a la matriz compuesta por los coeficientes y M’ a la ampliada:
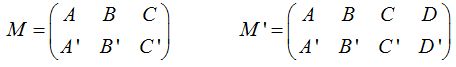
en la tabla siguiente resumimos los casos posibles:

23.23 ¿Cuál es la posición relativa de los planos:
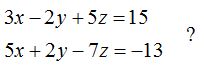
Respuesta: Secantes
Solución
El rango de coeficientes
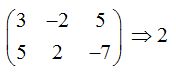
El rango de la ampliada:
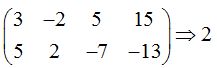
Estos dos planos se cortan.
23.24 ¿Cuál es la posición relativa de los planos:
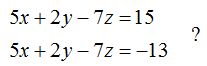
Respuesta: Paralelos
Solución
El rango de coeficientes
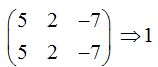
El rango de la ampliada:
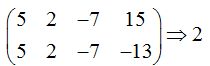
Como:
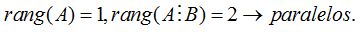
Solución
El rango de coeficientes
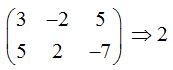
El rango de la ampliada:
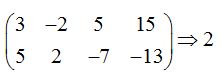
23.25 ¿Cuál es la posición relativa de los planos:
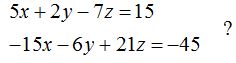
Respuesta: Coincidentes.
Solución
Verás que tanto el valor del rango de la matriz formada por los coeficientes como el valor del rango de la ampliada valen 1, lo que significa que son coincidentes. Los datos del 2º plano dependen de los del 1º multiplicados por 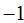 .
.
23.25 ¿Cuál es la posición relativa de los planos:
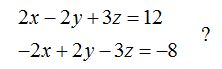
Respuesta: Paralelos.

