Posiciones Relativas de dos Planos. Rango de una Matriz
¿EXISTE ALGÚN MODO DE CÁLCULO PARA CONOCER EL RANGO DE UNA MATRIZ?
Claro que sí. Dirígete a MATRICES Y DETERMINANTES y encontrarás el método de Gauss.
A veces, si no tenemos un método, puede llevarnos tiempo en conocer el número de filas o columnas linealmente independientes.
Vamos a hacer paso a paso la deducción del rango de una matriz haciendo uso del menor de una matriz o submatriz.
Menor de una matriz es una parte de ella, es decir, tenemos en cuenta parte de ella. No tenemos en cuenta alguna/s fila/s y columna/s.
filas, tendrá también columnas y llamaremos a su determinante menor de orden n de la matriz propuesta.Tenemos la matriz:
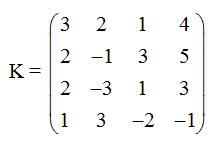
Elegimos un menor de orden 2 ( 2 filas, 2 columnas).
Tomamos los dos primeros datos de las dos primeras filas:
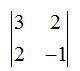
Hallamos el valor de su determinante, si nos da un valor distinto de cero quiere decir que su rango es dos.
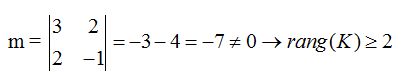
Si el valor del determinante es cero significa que hay filas o/y columnas dependientes. Como este no es el caso, tomamos un menor de orden 3:
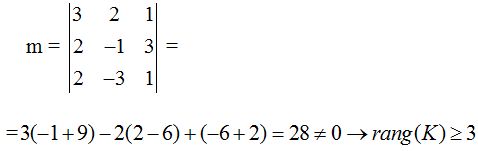
Como el resultado del determinante no es cero, hemos de continuar tomando el menor de orden 4:
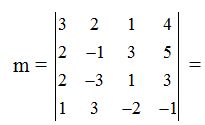
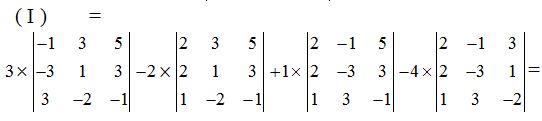
Calculamos los cuatro determinantes:
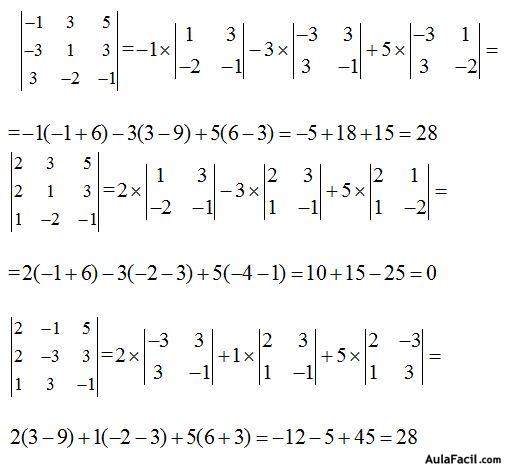
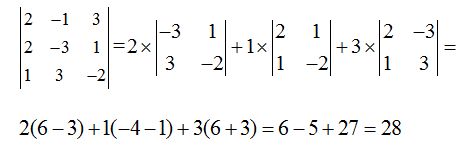
Estos valores los sustituimos en ( I ):
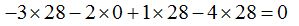
Como el valor del determinante es cero, el rango es el último obtenido hasta este momento, es decir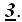 
23.22 ¿Cuánto vale el rango de la matriz:
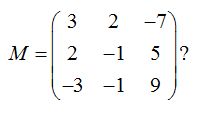
Respuesta: rang(M) = 3
