Posiciones Relativas de dos Planos.
2) Otro método para determinar la posición relativa de dos planos en el espacio se basa en determinar el rango de la matriz correspondiente a cada uno de ellos, tanto a la formada por los coeficientes de las variables como a la matriz ampliada que es aquella en que se incluyen los términos independientes en la anterior, por ejemplo:
Si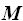 
es la matriz formada por los coeficientes de las variables del sistema y 
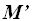la matriz que incluye a los términos independientes:
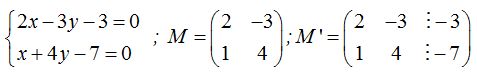
que podemos escribirla:
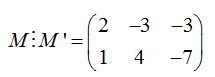
Recordemos:
Rango: Número de filas o columnas independientes de una matriz:
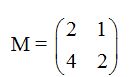
Si observas la matriz M verás que la segunda fila depende de la
, basta que multipliques por 2 a cada dato.
Luego rango vale 1.
23.19 ¿Cuánto vale el rango de la matriz:
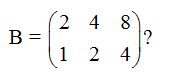
Respuesta: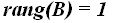 
23.20 ¿Cuánto vale el rango de la matriz:
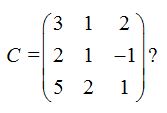
Respuesta: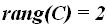 
Solución
La 
fila depende de la suma de las otras dos. Son independientes la 
y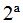 
filas.
23.21 ¿Cuánto vale el rango de la matriz:
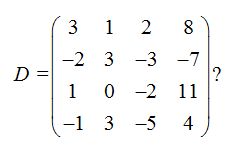
Respuesta: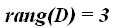 
Solución
La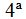 
fila depende de los valores de la 
+ 
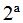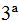lo que significa que existen 3 filas independientes.
