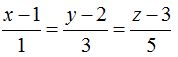Posición relativa de dos rectas en el Espacio.Pasar de la Ecuación de una recta en el Espacio.
PASAR DE LA ECUACIÓN DE UNA RECTA EN EL ESPACIO (PROCEDEDENTE DE LA INTERSECCIÓN DE DOS PLANOS) EN FORMA GENERAL O IMPLÍCITA, A SUS ECUACIONES EN FORMA VECTORIAL, PARAMÉTRICA Y CONTINUA:
Tras la realización del ejemplo siguiente, verás que se trata de algo muy sencillo.
Nos dan la siguiente ecuación de la recta en el espacio:
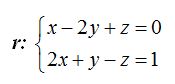
Para escribir la ecuación de la recta r en la forma vectorial, necesitas conocer un punto y el vector director.
Un punto cualquiera de la recta nos viene dado por los valores de x, y, z.
Resuelvo la ecuación dando a una incógnita un valor cualquiera, por ejemplo, 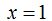
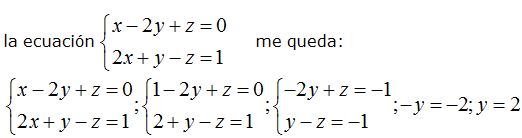
Sustituyendo los valores de 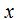 y de
y de 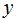 en la 1ª ecuación obtengo el valor de
en la 1ª ecuación obtengo el valor de 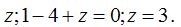
Un punto de la recta es 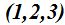 .
.
Al estudiar vectores en el espacio vimos que el producto vectorial de dos vectores equivale a un vector que tiene una dirección perpendicular a ambos y su sentido viene dado por el avance del tirafondos al girar en el sentido contrario a la marcha de las agujas de un reloj del primer vector al segundo por el camino más corto.
Ahora calculo el vector director y para ello debo conocer los vectores normales de las dos ecuaciones:
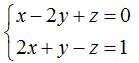
También estudiamos que el valor del producto vectorial de dos vectores es:
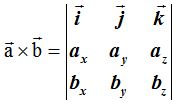
Siendo los datos de las filas 2ª y 3ª las componentes de los vectores 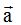 y
y 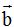 .
.
Estas componentes son los coeficientes respectivos de cada variable que figuran en la ecuación implícita de la recta.
Según lo anterior, las componentes de los vectores 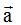 y
y 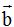 son :
son : 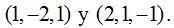
El vector director que es el producto de los vectores anteriores lo calculo:
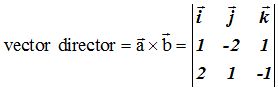
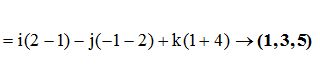
Si conocemos un punto (1,2,3) y el vector director (1,3,5) tenemos las respuestas de un modo sencillo:
Forma vectorial: 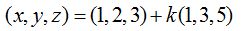
Forma paramétrica:
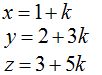
Forma continua: