Posición relativa de dos rectas en el Espacio
DADAS LAS ECUACIONES DE DOS RECTAS EN EL ESPACIO FORMA GENERAL SABER SU POSICIÓN RELATIVA:
Tal como lo hicimos con los planos, estudiando los rangos de las matrices lo haremos con las rectas en el espacio cuyo resumen lo tienes la tabla que tienes a continuación:

Vamos a realizar unos ejemplos que más adelante se te propondrán:
1.- ¿Cuál es la posición relativa de las rectas:
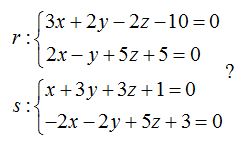
Solución
Formamos las matrices M y M’:
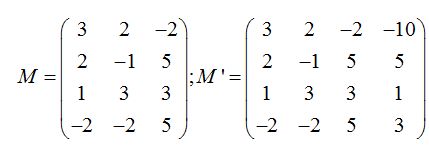
Resolvemos tomando la matriz ampliada ya que nos incluye a la formada por los coeficientes.
Al final, tenemos en cuenta los datos correspondientes a las 3 primeras columnas para determinar si son ceros o no todos los valores correspondientes a una fila.
El cálculo, aunque sencillo, explicado al estudiar el capítulo dedicado a Matrices y Determinantes es bastante laborioso. Siempre puedes encontrar en Internet algún programa que te permita realizar el cálculo con solo introducir los datos.
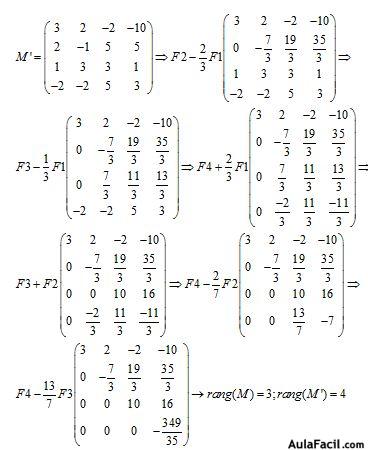
Vemos que los datos que corresponden a la matriz M tienen rango 3 (no tenemos en cuenta los términos independientes) y 4 el rango de la ampliada lo que quiere decir que las rectas se cruzan.
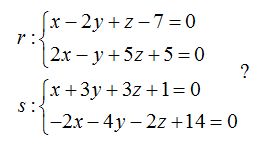
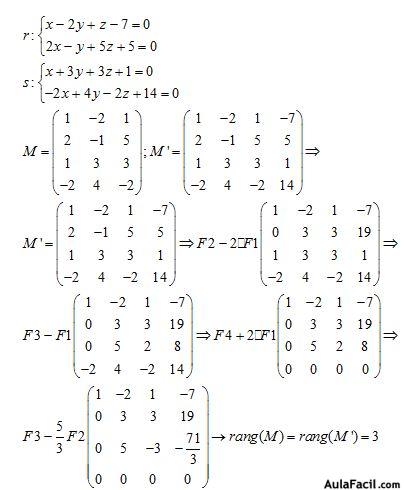
LAS RECTAS SE CORTAN EN UN PUNTO

