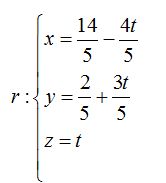Otro modo de pasar de una Ecuación en forma implícita a paramétrica
Supongamos que tenemos la recta:
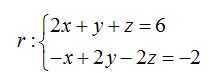
Un sencillo método para pasar a la forma paramétrica es dar a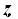 
el valor de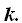 
Sustituimos:
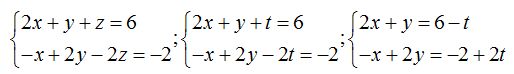
Igualamos las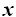 
y hacemos operaciones:
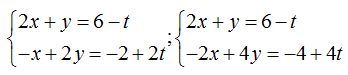
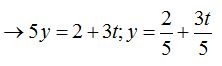
Calculamos el valor de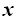 
sustituyendo, en la primera igualdad 
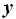por el valor que acabamos de obtener :
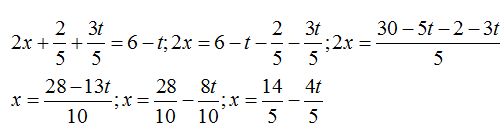
La ecuación de la recta en la forma paramétrica es:
