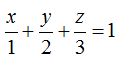Ecuación Segmentaria

En este caso, el plano corta a los 3 ejes. 
La intersección del plano con cada uno de los ejes nos da el valor de las coordenadas de cada punto.
Podemos tratar a esta forma como un caso particular de la ecuación del plano cuando conocemos tres puntos.
En la figura siguiente tenemos representado este plano que corta a los tres ejes:

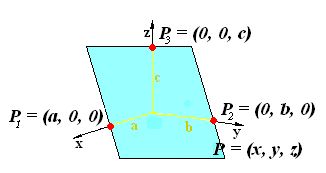
Como vemos en la figura, el plano corta a los ejes en los puntos:

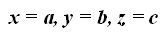
El punto P es uno cualquiera del plano cuyas coordenadas son: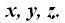 

El resto de los valores los obtenemos de:

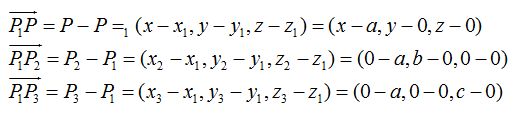
Para calcular la ecuación hacemos uso de lo estudiado en la ecuación del plano cuando conocemos tres puntos:

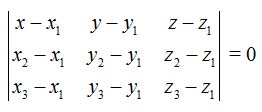
Sustituimos los valores de las nuevas coordenadas:

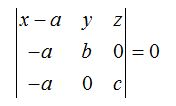
Resolvemos el determinante:

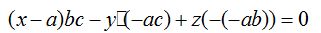
Hacemos operaciones:

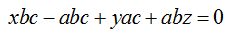
Dividimos cada término por abc:

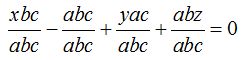
Simplificamos:

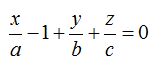
Pasamos el 1al segundo miembro de la igualdad y obtenemos la ecuación del plano en la forma segmentaria:

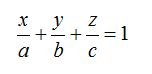
23.10  Escribe la ecuación del plano, en su forma segmentaria, que pasa por los puntos:

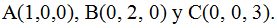
Respuesta: