Ecuación del plano que pasa por tres puntos

Tenemos un plano que pasa por los puntos cuyas componentes son, respectivamente:

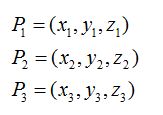
Los vectores representamos en la figura siguiente:

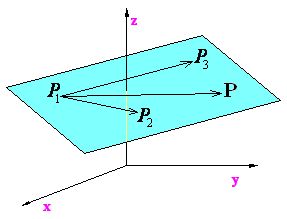
Un punto cualquiera del plano lo representamos con P, cuyas componentes desconocidas son: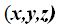 

Sabemos que dos puntos determinan un vector, por ejemplo, el 
vector:

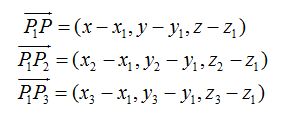
Hemos estudiado que la forma implícita de la ecuación del plano es:  

Si a las componentes de los vectores 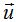 y 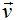los sustituimos por las componentes de cada uno de los tres puntos del plano que conocemos, obtenemos:

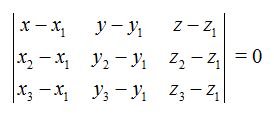
23.9   Escribe la ecuación del plano que pasa por los puntos: :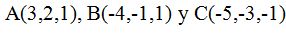

Respuesta: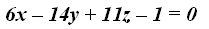 

Solución

Las coordenadas de un punto cualquiera del plano son: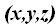 

Las coordenadas del punto 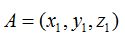que corresponden a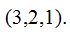 

Las coordenadas del punto 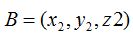que corresponden a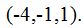 

Las coordenadas del punto 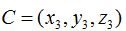que corresponden a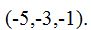 

Sustituyendo valores en:

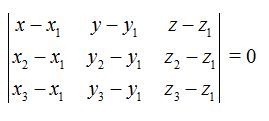
obtenemos:

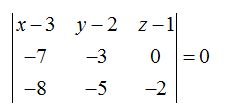
El ejercicio 23.8 corresponde también a esta solución.