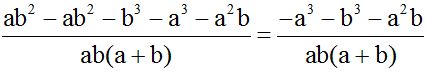Operaciones con Fracciones Algebraicas II
10.9 Calcula:
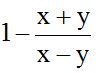Respuesta: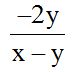 
Solución:
Igual al anterior, excepto que en lugar de sumar, ahora se trata de una diferencia y debes tener mucho cuidado con el signo menos delante de una fracción. El signo menos delante de una fracción le afecta solamente al numerador, y al sumar o restar con otros valores, se cambia de signo a cada término:
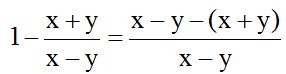
El denominador común será (x – y).
Le multiplico por 1 y queda x – y. Luego tienes el signo menos, que lo escribimos. Al segundo numerador lo encerramos entre paréntesis y le multiplicamos por 1 porque (x – y) entre (x – y) obtenemos 1.
Ahora quito el paréntesis del numerador:
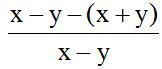
Recuerda que un signo menos delante de un paréntesis, al quitarlo, cada término que había dentro del paréntesis cambia de signo:
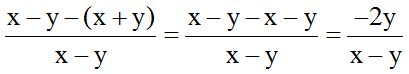
10.10 Resuelve:
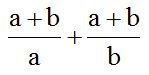Respuesta: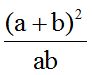 
Solución:
El común denominador será ‘ab’.
Al primer numerador le multiplicaremos por ‘b’ porque
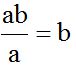
Al segundo numerador le multiplicamos por ‘a’ porque
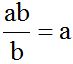
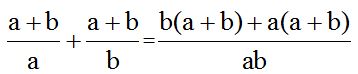
Quitamos paréntesis multiplicando el valor que está fuera por cada uno de los que están dentro:
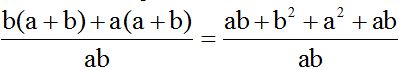
Reducimos términos semejantes y ordenamos los términos:
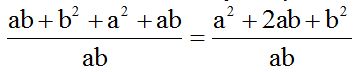
El numerador veo que procede de la suma de dos números al cuadrado:
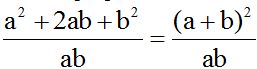
Otra solución sería, a partir de:
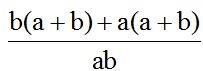
veo que en el numerador tengo dos términos que tienen el factor común (a + b). Saco factor común a (a + b):
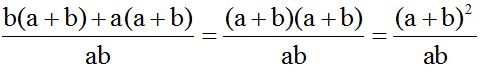
10.11 Resuelve:
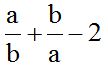Respuesta: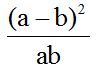 
10.12 Calcula:
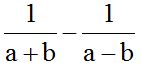Respuesta: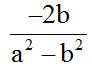 
Solución:
El denominador común, válido, para ambas fracciones será (a + b)(a – b).
Es como si tuvieras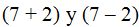 
El m.c.m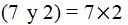 
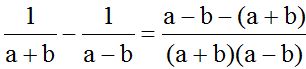
Al numerador de la segunda fracción que lleva el signo menos por delante, al multiplicarle por (a + b), escribimos el resultado del producto dentro de un paréntesis, para después, con mas seguridad, quitar el paréntesis cambiando de signo a cada término que se encuentre dentro del paréntesis y reducir los términos semejantes.
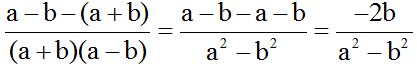
10.13 Calcula:
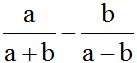Respuesta: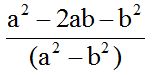 
Solución:
El denominador válido para ambas fracciones será el producto de los dos denominadores (a + b)(a – b); es como si tuvieses (5 +2) y (5 – 2), es decir, 7 y 3. El menor número múltiplo de ambos es: 7 X 3
Al dividir (a + b)(a – b) entre (a + b):
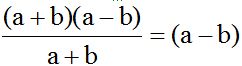
y ese cociente lo multiplicamos por ‘a’.
Lo mismo hacemos con el segundo denominador: (a + b)(a – b) entre (a – b) y el cociente lo multiplicamos por su numerador ‘b’:
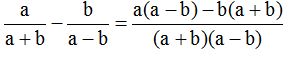
10.14 Calcula el valor de:
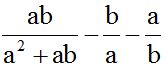Respuesta: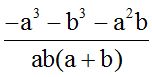 
Solución:
Analizamos lo que podemos hacer encada fracción y vemos que en el primer denominador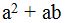 
podemos sacar factor común a ‘a’:
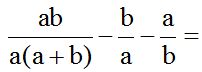
En el primer numerador tenemos el producto ‘ab’ y en el denominador tenemos 2 factores: ‘a’ y ‘(a+b)’. Podemos simplificar el factor ‘a’ del numerador con el factor ‘a’ del denominador y nos quedaría:
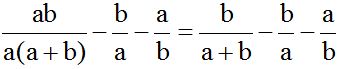
Calculamos el m.c.m. de los denominadores compuestos por los valores:(a+b), a y b. Imagina que a = 7 y b = 3: tendrías que calcular el m.c.m. (10, 7 y 3) que sería el producto de los 3.
El m.c.m. de (a+b), a y b es ab(a+b) y este valor lo dividimos por cada denominador y el cociente lo multiplicamos por su numerador correspondiente:
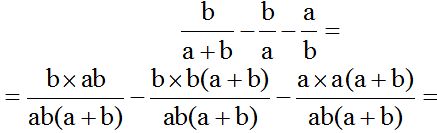
Para ahorrar trabajo, escribimos en una sola fracción porque sus denominadores son iguales. Cuida el orden alfabético y cuidado con los signos menos delante de un paréntesis al quitar a éstos:
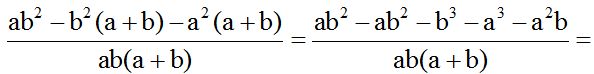
Reducimos los términos semejantes que podamos:
