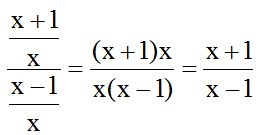Multiplicación y división de fracciones algebraicas
Basta que tengas en cuenta como se multiplican y dividen las fracciones como estudiaste hasta ahora. Con tener en cuenta, respecto a la parte literal, que, para multiplicar potencias de la misma base se suman los exponentes y para dividir se restan, es suficiente.
10.21 Halla el valor de:
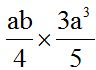Respuesta: 
.
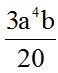Solución:
Para multiplicar fracciones se halla el producto de numeradores y se divide por el producto de denominadores. Si se puede, se simplifican factores comunes:
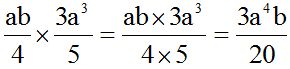
10.22 Calcula el producto:
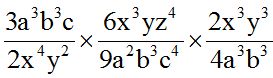Respuesta: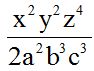 
Solución:
Multiplicamos la parte numérica primero y luego la parte literal sumando los exponentes de las potencias de la misma base:
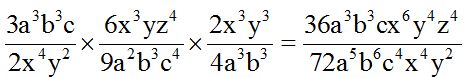
Dividimos la parte numérica primero y luego la parte literal restando los exponentes de las potencias de igual base y su resultado lo colocamos donde el exponente era mayor:
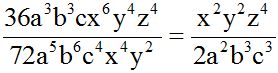
10.23 Halla el producto de:
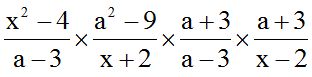Respuesta: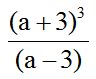 
Solución:
Indicando los productos notables y simplificando factores comunes:
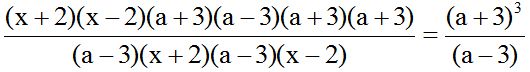
10.24 Halla el producto de:
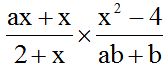Respuesta: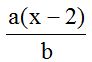 
Solución:
Antes de comenzar a hacer el producto debes fijarte en cada término del numerador y denominador para ver si hay factores comunes para después simplificar y trabajar con valores más pequeños.
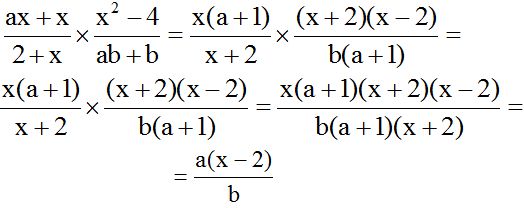
10.25 Calcula el producto:
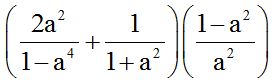Respuesta: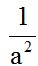 
Solución:
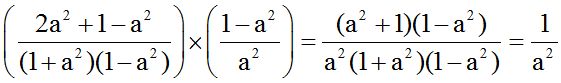
10.26 Divide:
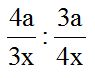Respuesta: 
.
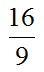Solución:
Recuerda que para dividir fracciones puedes multiplicar la primera por el inverso de la segunda, es decir, “darle vuelta” a la segunda fracción, que equivale a poner el numerador como denominador y a éste como numerador.
También puedes multiplicar el primer numerador por el segundo denominador y este producto dividir entre el producto del primer denominador por el numerador de la segunda fracción.
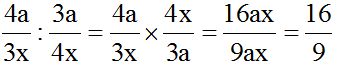
10.27 Divide:
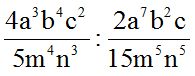Respuesta: 
.
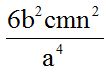10.28 Calcula:
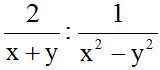Respuesta: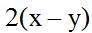 
Solución:
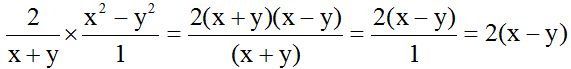
10.29 Calcula:
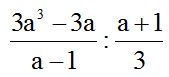Respuesta: 
Solución:
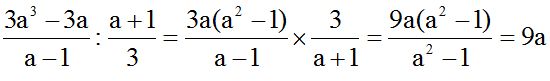
10.30 Halla el cociente:
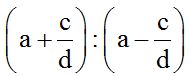Respuesta: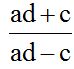 
Solución:
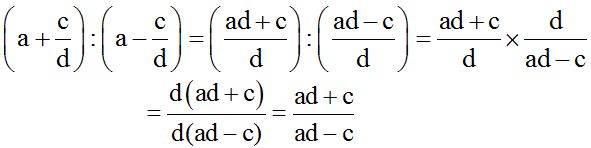
10.31 Calcula:
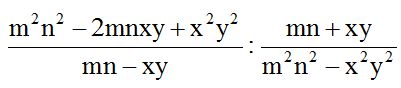
Respuesta: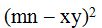
Solución:
Resolvemos teniendo en cuenta los productos notables: el cuadrado de la diferencia de dos números y suma de dos números por su diferencia igual a la diferencia de sus cuadrados.
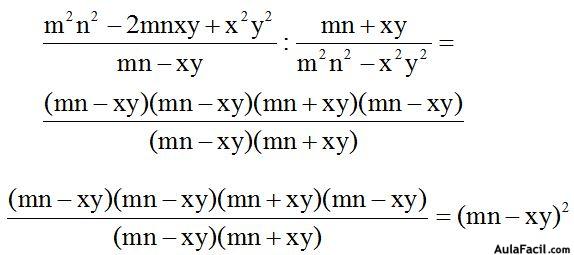
10.32 Resuelve :
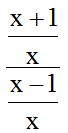Respuesta: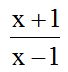 
Solución:
Siempre que tengas una fracción dividida por otra del tipo:
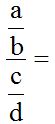es lo mismo que 
.
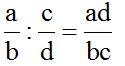En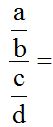 
los términos extremos son ‘a’ y ‘d’ (1º y 4º) y los términos medios ‘b’ y ‘c’
Este cálculo es muy sencillo, es suficiente que retengas: producto de extremos dividido por el producto de medios: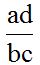 
Si aplicamos cuanto acabamos de decir al enunciado del presente ejercicio tendríamos:
