Operaciones con números complejos en forma binómica

En esta lección veremos como se realizan las operaciones con números complejos en forma binómica.

Suma

Para sumar dos números complejos z1= a+bi y z2=c+di se suman las partes reales y las partes imaginarias respectivamente tal y como se indica a continuación.

z1+z2= (a + bi) + (c+di) = (a+c)+(b+d)i

Ejemplo: Sumar los números complejos z1=2+2i y z2=3+i

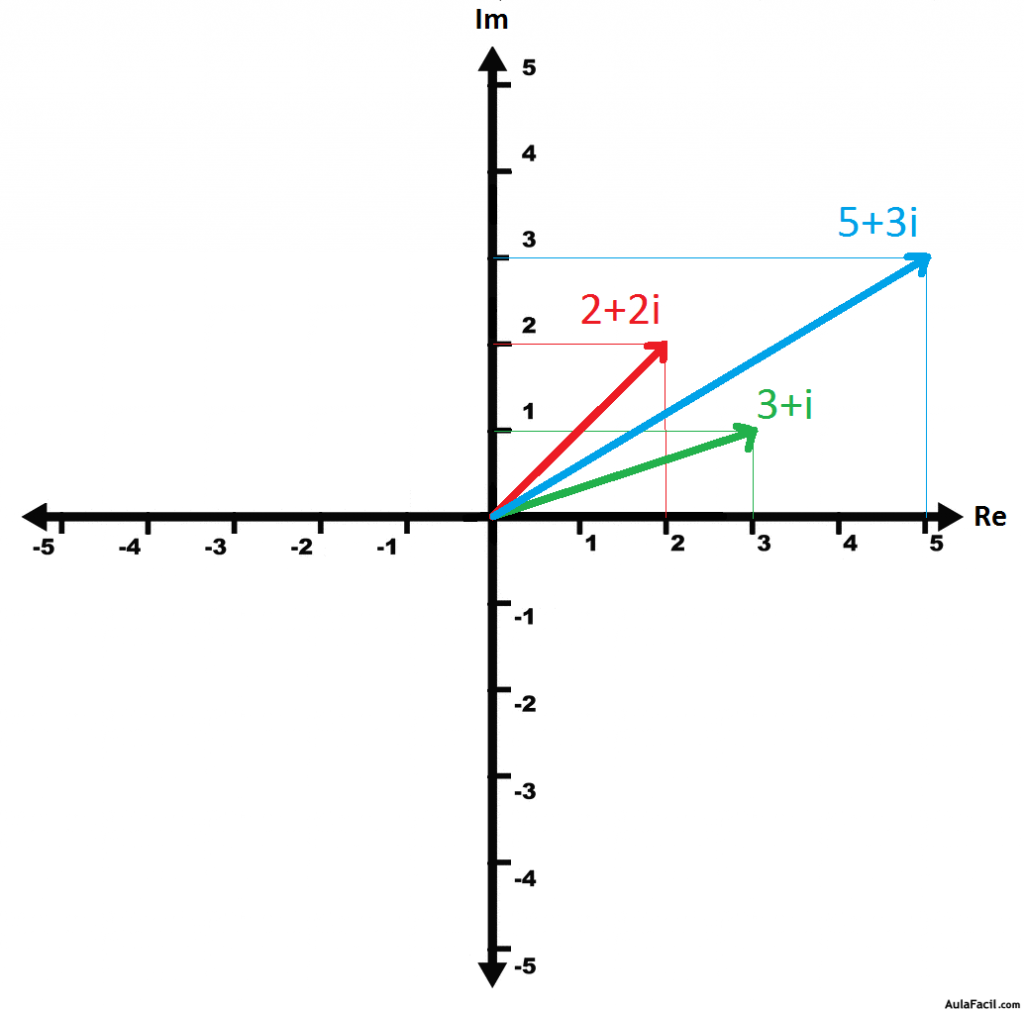
z1+z2=2+2i+3+i= (2+3)+(2+1)i= 5+3i

En la figura siguiente se muestra la representación gráfica de la suma de los dos números complejos que se muestran en el presente ejemplo:

Resta

Para restar dos números complejos z1= a+bi y z2=c+di se realiza tal y como se indica a continuación.

z1 - z2= (a + bi) - (c+di) = (a-c)+(b-d)i

Ejemplo: Dados los números complejos z1=5-i y z2=1+4i calcular z1-z2

z1-z2 = (5-i) - (1+4i) = 5-1 + (-1-4)i = 4 - 5i

Multiplicación

Para multiplicar dos números complejos z1= a+bi y z2=c+di se realiza tal y como se indica a continuación.

z1.z2= (a + bi)  (c+di) = a.c + adi + bci + bdi² como i²= -1

z1-z2 = (ac-bd) +(ad+bc)i

Ejemplo: multiplicar los números complejos z1= 2 + i  y  z2 = 4+5i

z1.z2 = (2x4-1x5) + (2x5 + 1x4)i = 3 + 14i

También se puede realizar la operación multiplicando cada uno de los términos de a+bi y c+di y simplificando y agrupando sabiendo que i²= -1

Ejemplo: 

(3+2i).(1+i) = 3x1 + 3i +2i +2i² = (3-2) + (3+2)i = 1 +5i

División

Para dividir dos números complejos a + bi y c + di es necesario definir el conjugado de un número complejo en primer lugar.

Si z= a + bi es un número complejo entonces el número complejo conjugado de z es 

Así por ejemplo en número complejo conjugado de 1+6i es el número complejo 1-6i.

si queremos dividir dos números complejos a + bi entre c+di multiplicamos y dividimos por el número complejo conjugado de c+di, es decir c-di

Ejemplo: Realizar la siguiente división de dos números complejos

Potencias de i

Sabemos que i²=-1 así podemos determinar las potencias de i

Se puede observar que los resultados de las potencias de i se repiten de 4 en 4. Para saber el resultado de una potencia de i se divide el exponente entre 4 y el resto equivale a la potencia que se quiere determinar.

Ejemplo: Calcular i⁵⁷

57/4=14 y resta 1 ya que 14.4=56

entonces i⁵⁷=i

Ejemplo: calcular i¹⁰³

103/4=25 y restan 3 

por lo tanto i¹⁰³=i³=-i

A continuación se encuentran unos ejercicios de autoevaluación