Números complejos en forma polar

Sea un número complejo expresado en forma binómica a+bi entonces se define el módulo del número complejo al valor open vertical bar z close vertical bar equals square root of a squared plus b squared end root y el argumento del número complejo θ se expresa de la forma

 theta equals a r c t g open parentheses b over a close parentheses

Gráficamente el módulo mide la longitud del vector que representa al número complejo y el argumento θ es el ángulo que forma el vector con el eje de abscisas.

En la figura que se muestra a continuación se puede observar el módulo y el argumento de un número complejo.

representacion complejos

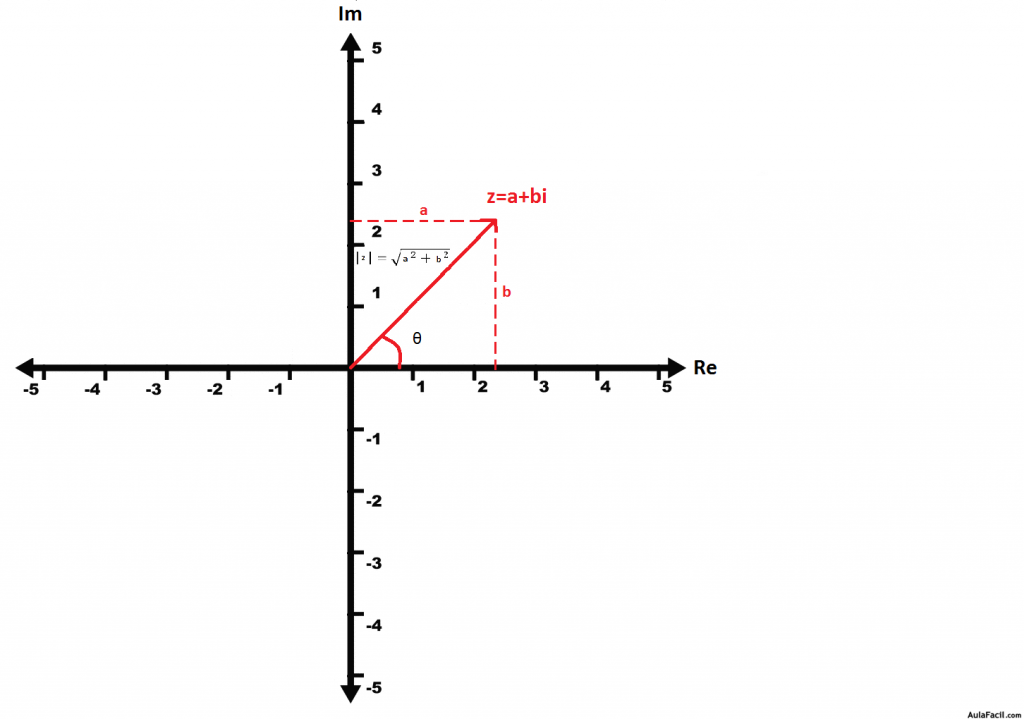
Representación complejos

La expresión de un número complejo a + bi en forma polar es de la forma

 open vertical bar z close vertical bar subscript theta

Si observamos la figura de la misma se puede deducir que

 a equals open vertical bar z close vertical bar times cos theta y b equals open vertical bar z close vertical bar times s e n theta

Es decir, conocidos el módulo│z│y el argumento θ, un número complejo en forma binómica se puede expresar de la forma:

open vertical bar z close vertical bar subscript theta equals open vertical bar z close vertical bar open parentheses cos theta plus i s e n theta close parentheses

Normalmente el argumento θ  se expresa en radianes, aunque también se puede expresar en grados.

Ejemplo: Expresar en forma polar los números complejos

a right parenthesis space 1 plus square root of 3 i b right parenthesis space 1 plus i

----------------------------------------------------------------

a right parenthesis space 1 plus square root of 3 i

open vertical bar z close vertical bar equals square root of 1 squared plus 3 end root equals 2 theta equals a r c t g open parentheses fraction numerator square root of 3 over denominator 1 end fraction close parentheses equals straight pi over 3 p o r space l o space tan t o space e l space n ú m e r o space c o m p l e j o space e n space f o r m a space p o l a r space e s 2 subscript straight pi over 3 end subscript

b right parenthesis space 1 plus i open vertical bar z close vertical bar equals square root of 1 squared plus 1 squared end root equals square root of 2 theta equals a r c t g open parentheses 1 over 1 close parentheses equals straight pi over 4 p o r space l o space tan t o space e l space n ú m e r o space c o m p l e j o space e n space f o r m a space p o l a r space e s square root of 2 subscript straight pi over 4 end subscript

Ejemplo: Sea el número complejo 2 subscript straight pi divided by 4 end subscript expresarlo en forma binómica2 subscript straight pi divided by 4 end subscript equals 2 open parentheses cos straight pi over 4 plus i s e n straight pi over 4 close parentheses equals square root of 2 plus square root of 2 i

 

A continuación se proponen unos ejercicios de autoevaluación

Inicia sesión para hacer seguimiento de tus autoevaluaciones
  1. Expresar en forma binómica 3π
  2. Expresar en forma binómica 411π/6
  3. Expresar en forma polar el número -3i
  4. Expresar en forma polar el número -2-2i
Corregir   Ver Solución   Limpiar

 

 

 

Contenidos que te pueden interesar
Este sitio usa cookies para personalizar el contenido y los anuncios, ofrecer funciones de redes sociales y analizar el tráfico. Ninguna cookie será instalada a menos que se desplace exprésamente más de 400px. Leer nuestra Política de Privacidad y Política de Cookies. Las acepto | No quiero aprender cursos gratis. Sácame