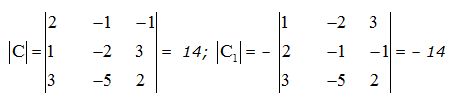Propiedades de los Determinantes. Ejercicios #38 y 39

Ejercicio #38  

Haciendo uso del modo que acabamos de explicar: ¿Cuánto vale

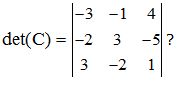
Respuesta: det(C) = 14

Ejercicio #39    

Haciendo uso del modo más sencillo para ti ¿Cuánto vale

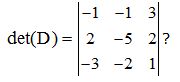
Respuesta: det (D) = – 48 

¿Cómo calculamos el valor de un determinante de orden superior a 3?

Esto se complica un poco, basta que te fijes que para pasar de orden 2 a orden 3 nos ha exigido realizar mayor número de operaciones.

Para reducir, por lo menos, el número de operaciones cuando tratamos de determinantes de un orden superior a 3, nos exige tener un mayor conocimiento de los determinantes y para ello, comenzamos a estudiar sus propiedades.

PROPIEDADES DE LOS DETERMINANTES

1ª) Un determinante es nulo si tiene:

a.- Dos filas iguales:

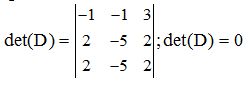
b.- Dos columnas iguales:

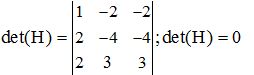
 c.- Si todos los elementos de una fila o columna son ceros:

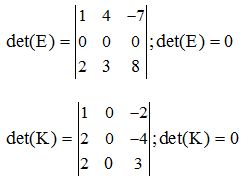
e.- Si los elementos de una fila o columna proceden del producto o cociente de un número por los elementos de otra fila o columna el valor del determinante es 0:

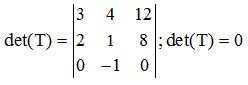
La 3ª columna procede de multiplicar a la 1ª por 4.

2ª)  El valor de un determinante triangular es igual al producto de la diagonal principal:

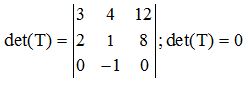
3ª) El valor del determinante de una matriz y el de su traspuesta tienen el mismo valor:

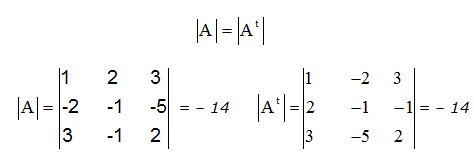
4ª) En un determinante, si cambias dos líneas paralelas (filas o columnas), el determinante cambia de signo: