Cómo calculamos el valor de una determinante de orden 3. Ejercicio #37

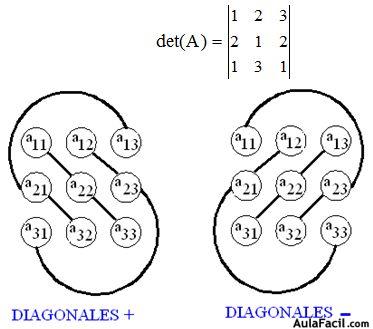
Multiplicamos los elementos de las diagonales principales y vamos sumando los productos obtenidos:
 

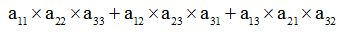
Hallamos la diferencia de las dos cantidades obtenidas y será el valor del determinante:
 

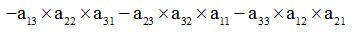
Pasemos a la práctica:

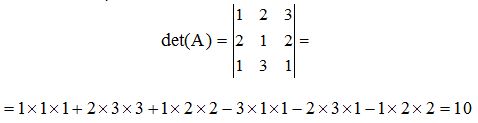
Creo que calcular de este modo el valor de un determinante de tercer orden se puede olvidar al cabo de unos días.

Posiblemente, hacerlo del siguiente modo:

1) Escribes el determinante sea más fácil tanto de operar como recordar:

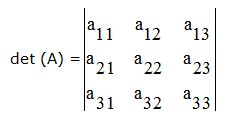
Escribes a continuación, detrás de la 3ª columna, las dos primeras:

Ahora realizas las sumas de los productos de los elementos de la diagonal principal que son las líneas trazadas de izquierda a derecha.

Haces lo mismo con las diagonales que van de derecha a izquierda como lo representado en la figura siguiente:

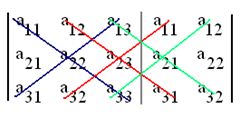
Verás que coincide con lo dicho anteriormente:

Respuesta: det (B) = 9

Solución

Escribimos primeramente la suma de los productos de las diagonales principales y en segundo lugar vamos restando el producto de las diagonales secundarias:
 

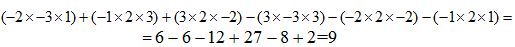
Otro sencillo modo de calcular los determinantes de orden 3:

1) Escribes el determinante del modo siguiente:

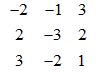
2) Escribes a la derecha el resultado de las dos diagonales comenzando siempre por la principal:

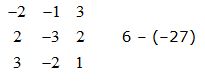
3) Ahora anula la primera línea y escríbela como la tercera línea:

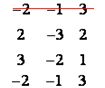
Y vuelve a hallar los valores (sin tener en cuenta a la fila anulada) de las diagonales colocando los resultados a continuación de los obtenidos en el paso 2):

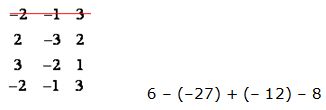
4) Haz lo mismo con la 2ª fila, anúlala y pásala como tercera fila y calculamos nuevamente los valores de ambas diagonales:

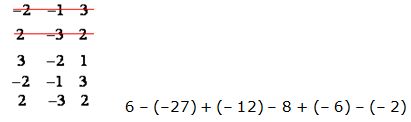
5) Por fin, llegamos a la fila 3ª y última y si volviéramos a hacer lo que estamos realizando, es decir, anularla y pasarla debajo estaríamos con el mismo determinante propuesto al principio:

Esto quiere decir que en el paso 4) terminamos. Nos queda hallar el total de las sumas parciales: 6 + 27 – 12  –  8  – 6 + 2 = 9