Ejercicios #43, 44 y 45
Ejercicio #43
Sin hacer ninguna operación, indica el valor de la determinante siguiente:
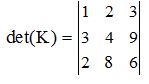
Respuesta: det (K) = 0
Solución
La 3ª columna es proporcional a la 1ª. Basta que a ésta multipliques por 3 para obtener la 3ª. Si dos líneas paralelas son proporcionales el determinante vale cero.
7ª) A los elementos de una fila o columna puedes decomponerles en dos sumandos. Con los sumandos obtenidos escribes dos determinantes (con cada uno de estos sumandos) permaneciendo los mismos elementos de las otras dos líneas que los repites en cada determinante.
La suma de los dos determinantes equivalen al determinante primitivo (sin descomponer en dos sumandos una determinada fila o columna).
Partimos del determinante:
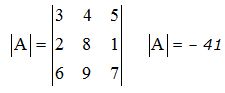
A los elementos de la 3ª fila los descomponemos en dos sumandos:
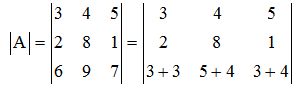
Con cada sumando creamos dos determinantes. El resto de los elementos los repetimos en cada determinante:
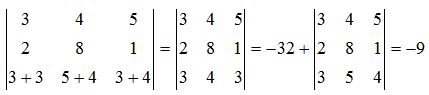

Ejercicio #44
Escribe el valor del determinante:
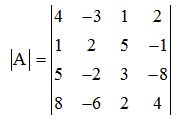
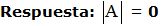
Solución
La fila 4ª es linealmente dependiente de la 1ª (la hemos multiplicado por 2).
Ejercicio #45
Si a los elementos de una fila de un determinante de orden 3 cuyo valor es 24 los multiplico por 3 ¿qué valor adquiere el nuevo determinante?
Respuesta: 72 (24 X 3)
Solución
Comprobamos:


