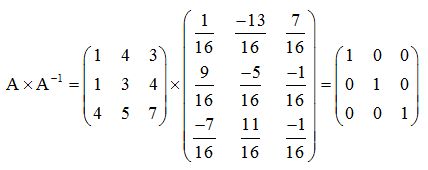Ejercicio #51. Matriz Adjunta, Matriz Inversa (III)

Ejercicio #51 

Calcula el valor del determinante:

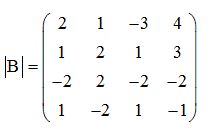
Matriz adjunta:

Matriz adjunta es la que obtenemos de sustituir a cada elemento por su adjunto.

Partimos de:

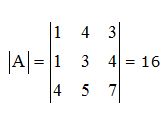
Sustituimos a cada elemento por su adjunto:

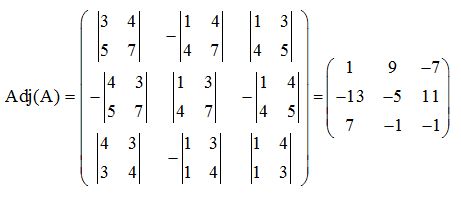
Matriz inversa (III):

Aunque anteriormente ya nos referimos a ella, ahora volvemos a estudiarla sirviéndonos de los determinantes.

Estudiamos anteriormente que el producto de una matriz por su inversa es igual a la matriz identidad.

Siendo A una matriz, estudiamos que:

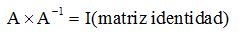
El cálculo de la matriz inversa cumple con:

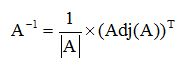
Vemos que la matriz inversa es igual al inverso de su determinante por la traspuesta de su matriz adjunta.

Vamos a llevar a cabo los pasos que nos indica la igualdad anterior.

Conocemos el valor de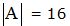 

La traspuesta de 

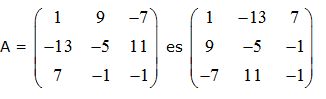
El inverso del determinante calculamos que era 16, luego su inverso: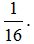 

Multiplicando 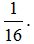 por cada elemento de la matriz nos quedará:

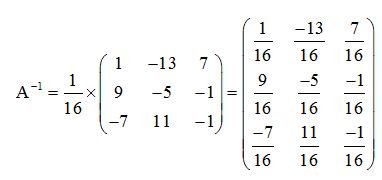
Comprobación:

Sabemos que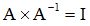  

Tenemos que obtener una matriz de orden 3 cuya diagonal principal contenga unos y el resto de los elementos sean ceros.`