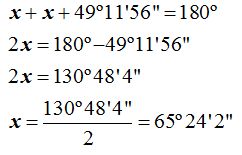Los Ángulos en la circunferencia -3
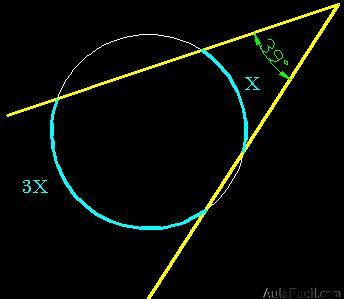
15.153 Calcula las medidas de los arcos que abarcan los lados de un ángulo exterior a una circunferencia de 39º sabiendo que un arco es el triple del otro.
Respuesta: 39º y 117º
Solución:
Si un arco mide xº el otro medirá 3x
Haciendo aplicación de la fórmula:
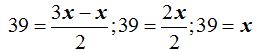
El arco menor mide 39º y el mayor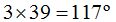 
15.154 Dos tangentes a una circunferencia forman un ángulo de 46º ¿Cuánto mide el menor de los arcos que forman en la circunferencia?
Respuesta: 134º
Solución
Al menor de los arcos le damos el valor X
El mayor medirá……………………….360 – X
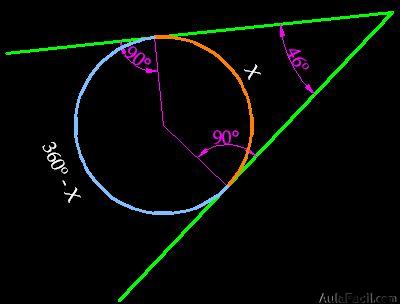
Aplicando la fórmula tendremos:
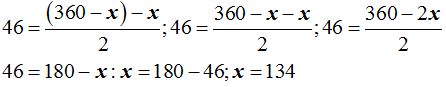
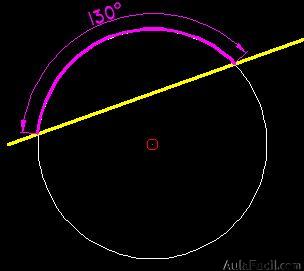
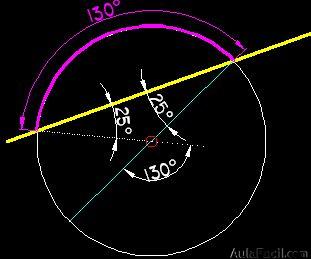
15.155 Trazamos una secante a una circunferencia y forma un arco de 130º. ¿Cuánto vale el ángulo cuyo vértice está en el punto donde se encuentran la secante y el diámetro de la circunferencia? Dibuja la figura.
Respuesta: 25º
Solución
En muchos problemas, si dibujamos bien la figura hemos conseguido más de la mitad de su solución. Es importante acompañar, siempre que sea posible, cada problema con su correspondiente figura.
Comenzamos a trazar la secante a la circunferencia y el arco de 130º:
Ahora le añadimos la diagonal (ha de pasar por el centro de la circunferencia y se une con uno de los extremos de la secante:
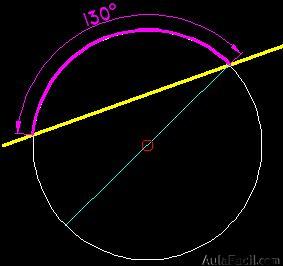
Si ahora unimos el otro extremo de la secante con el centro y prologamos la línea:
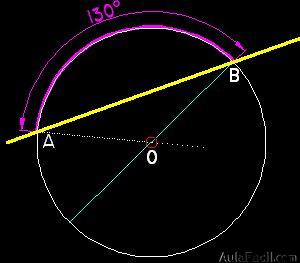
Compruebo que me queda el triángulo isósceles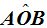 
cuyos ángulos los señalo del modo siguiente:
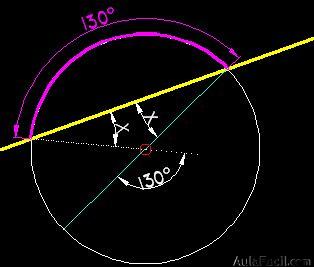
Como el ángulo central determina un arco igual al que abarcan sus lados conozco de este modo el valor de un ángulo del triángulo (por opuesto por el vértice) y los otros ángulos al ser iguales les doy el valor x a cada uno ellos, escribo la ecuación teniendo en cuenta que ka suma de los tres ángulos de un triángulo valen 180º:
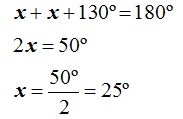
La figura completa será:
15.156 Una secante a una circunferencia crea un arco de 86º. ¿Cuánto valen los ángulos inscritos cuyos lados pasan por los extremos de la secante? Dibuja el contenido del texto.
Respuestas: 43º y 137º
Solución:
Trazamos la secante AB a la circunferencia con centro en O.
Dibujamos los lados del ángulo inscrito que valdrá la mitad del ángulo central sin importarnos el punto de la circunferencia que elijamos, siempre tendrá el mismo valor mientras nos refiramos al mismo arco.
Piensa que si tomamos los puntos de intersección de la secante a la circunferencia creamos dos arcos.
Estos dos arcos los consideramos a continuación:
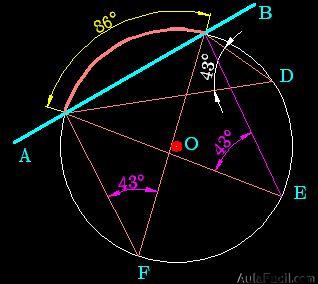
Los vértices en D, E y F valen lo mismo porque se refieren al mismo ángulo inscrito.
Todos ellos valen la mitad del central y éste equivale al arco que abarcan sus lados.
Otra solución:
Otra respuesta la podemos obtener si elegimos al arco mayor como correspondiente al ángulo central:
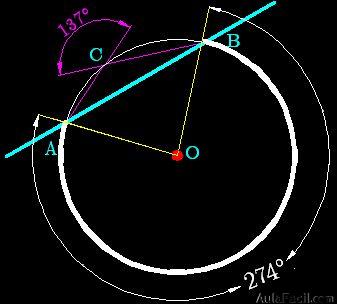
En este caso el ángulo central abarca un arco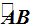 
de 274º lo que quiere decir que el inscrito en el punto C de la circunferencia vale la mitad, es decir, 137º.
15.157 Unimos por medio de una recta dos puntos A y C de una circunferencia y creamos un arco de 130º48’4’’. Por ambos puntos trazamos desde el punto exterior B a la circunferencia dos tangentes. ¿Cuánto valen los ángulos cuyos vértices se hallan en A, B y C?
Respuestas: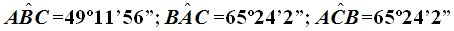
Solución:
Los arcos en los que la cuerda AC ha dividido a la circunferencia miden 130º48’4” y 229º11’56”.
El ángulo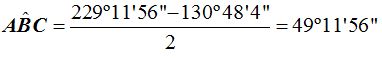 
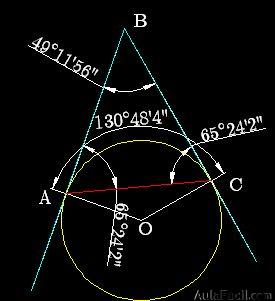
Los ángulos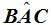 
y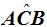 
son iguales porque el triángulo 
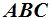es isósceles. Si damos el valor de x a cada uno de ellos, podemos escribir la ecuación:
