Fórmula para el cálculo de la longitud de una Circunferencia - Elementos de una Circunferencia
Has visto hasta este momento que en lo que se refiere a la circunferencia hemos utilizado 2 valores: diámetro y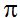 
No es costumbre utilizar el diámetro, sino el valor del radio.
Mientras no digamos lo contrario, a partir de este momento, usaremos el radio cuando nos refiramos a la circunferencia. Recuerda que el radio es la mitad del diámetro.
La longitud de una circunferencia depende de dos valores, uno de ellos se mantiene invariable, el valor de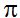 
y el otro valor el del radio.
Cuanto mayor sea el valor del radio, mayor será la longitud de la circunferencia y el otro factor que aparece en todo los cálculos de longitudes de circunferencias y se mantiene siempre con el mismo valor sea grande como pequeña la figura es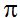 
La longitud de la circunferencia depende del tamaño del radio. El factor 
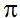se mantiene en el cálculo de las longitudes de todas las circunferencias.
Si representamos por L la longitud de una circunferencia y por r el valor del radio, diremos que:
Sería lo mismo que multiplicar el diámetro ( 2x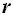
) por 3,1416 (
)
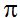15.127 Calcula la longitud de una rueda cuyo radio mide 3,5 dm. La respuesta debe contener 3 decimales.
Respuesta: 21,991 dm.
15.128 Una circunferencia tiene una longitud de 124,756 cm. ¿Cuánto vale el radio? (respuesta con 3 decimales).
Respuesta: 19,855 dm.
Solución:
Sustituyo los valores que conozco en la fórmula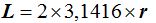
y obtengo: 
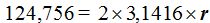de donde:
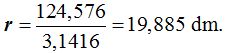
15.129 Una circunferencia cuya longitud vale 123,45 m. ¿cuál es el valor de su diámetro?
Respuesta: 39,295 dm.
ELEMENTOS DE UNA CIRCUNFERENCIA
Es necesario que aprendas los elementos de toda circunferencia:
1) centro. El punto del que equidistan todos los puntos de la circunferencia.
2) radio. Segmento que une el centro con cualquier punto de la circunferencia.
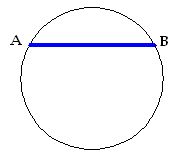
3) cuerda: Segmento que une dos puntos cualesquiera de la circunferencia sin que pase por el centro:
4) sagita: Segmento que une el centro de un arco de circunferencia con el punto medio de la cuerda que le corresponde:
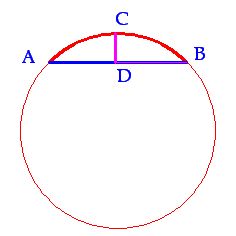
El segmento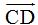 
es la sagita.
5) diámetro: Segmento o cuerda que une dos puntos cualesquiera de una circunferencia que pase por el centro de la circunferencia.
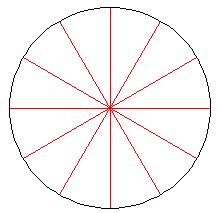
Todas líneas en rojo son diámetros.
6) ángulo central: Es el ángulo que tiene su vértice en el centro de la circunferencia y sus lados son radios de la misma.
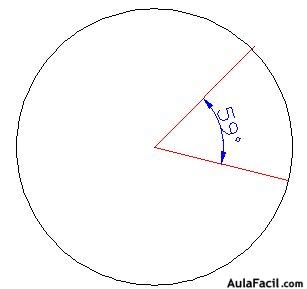
En este caso, el ángulo central vale 59º.
7) arco: Es una parte, una porción, un trozo comprendido entre dos puntos de la circunferencia:
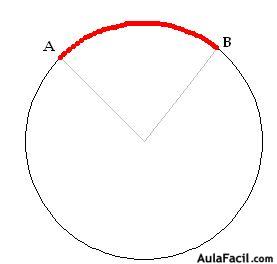
La curva comprendida entre los puntos A y B de la circunferencia, es la parte o porción de la misma que se llama arco.
