Posiciones relativas de un punto respecto a una Circunferencia
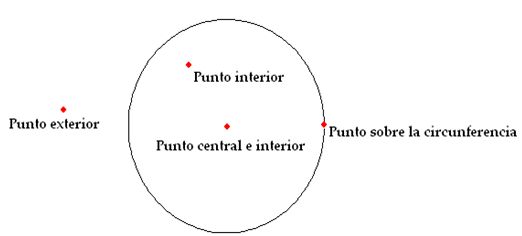
La posición de un punto con relación a una circunferencia puede ser triple:
1) Que el punto esté fuera de la circunferencia.
2) Que esté sobre la misma línea de la circunferencia.
3) Que el punto esté dentro de la circunferencia.
POSICIONES RELATIVAS DE UNA RECTA RESPECTO A UNA CIRCUNFERENCIA
Una recta respecto a una circunferencia puede ocupar las siguientes posiciones:
a) Si una recta no tiene ningún punto en común con una circunferencia la llamamos recta exterior a la circunferencia:
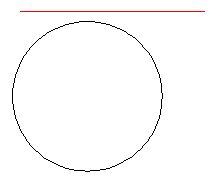
Como ves, la circunferencia y la recta no tienen ningún punto perteneciente a la vez, a ambas figuras.
b) Si una recta tiene un punto en común con una circunferencia decimos que se trata de una recta tangente a la circunferencia:
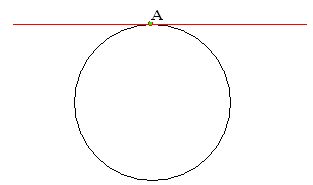
Tangente es una palabra que procede del latín y significa tocar,palpar.
La recta es tangente a la circunferencia en el punto A. Le toca en el punto A.
El punto A de la recta es también un punto de la circunferencia, es decir, que el punto es común para la recta y para la circunferencia y se le llama punto de tangencia..
También podemos decir que una recta es tangente a una circunferencia cuando la distancia entre el centro de la circunferencia al punto común es igual al radio:
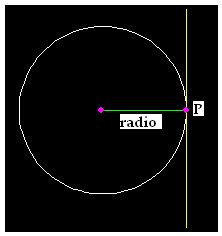
El punto P es común para la recta y para la circunferencia, y la distancia entre P y el centro de la circunferencia equivale al radio.
c) Si una recta tiene dos puntos comunes con una circunferencia decimos que se trata de una recta secante a la circunferencia.
La palabra secante que procede de la palabra latina secare significa cortar.
Podríamos decir también que una recta es secante a una circunferencia si le corta a ésta por dos puntos:
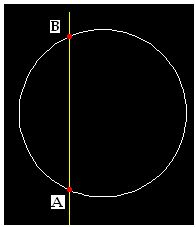
Observarás que la recta corta a la circunferencia en los puntos A y B a la circunferencia.
15.130 ¿Puedo trazar tres rectas tangentes a una circunferencia por el punto de tangencia? Razona la respuesta.
Respuesta: No, solamente una.
Razonamiento:
Observa la figura siguiente:
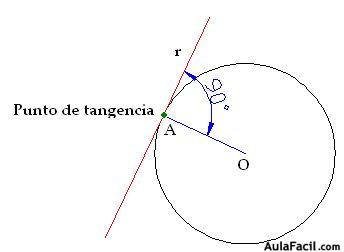
El radio OA es perpendicular a la recta r en el punto de tangencia por formar entre ambas (radio y recta) un ángulo de 90º, luego la recta r es tangente a la circunferencia en el punto A que está sobre la circunferencia.
Si trazamos otra recta, la recta s, como te muestra la figura siguiente, el punto de tangencia ha cambiado de lugar.
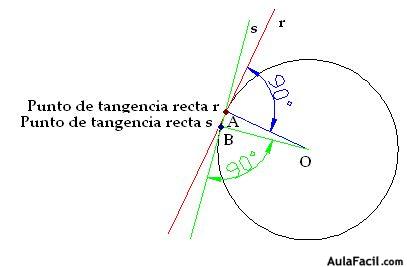
Ves que el radio OB forma un ángulo de 90º con la recta s, es decir, es tangente en el punto de tangencia B mientras que la recta r es tangente a la circunferencia en el punto A.
Tenemos dos rectas tangentes en puntos diferentes sobre la circunferencia.
Por cada recta que tracemos tendremos un nuevo punto de tangencia.
15.131 Desde un punto exterior a una circunferencia ¿cuántas tangentes a ella puedo trazar? Dibuja.
Respuesta: Dos tangentes.
Dibujo:
Lo vamos a hacer en partes:
1) dibujo una circunferencia y el punto exterior:
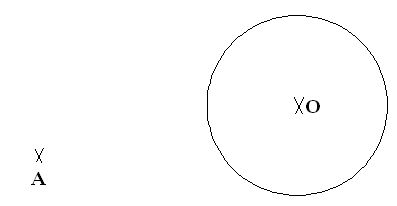
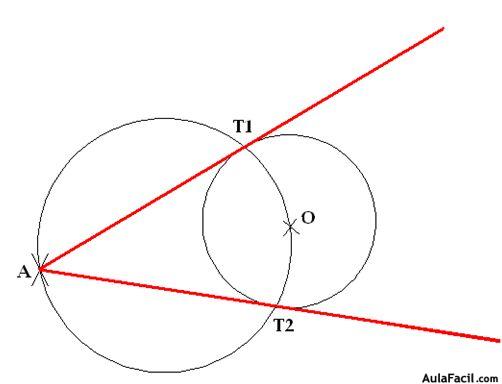
2) dibujo una segunda circunferencia que pase por el punto exterior A y por el centro de la circunferencia O:
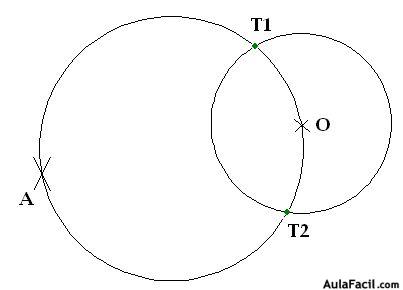
Los puntos T1 y T2 son los puntos de tangencia.
3) Ahora dibujo dos rectas que nacen en A y pasan por T1 y T2 y serán las tangentes a una circunferencia desde un punto exterior A: