Cálculo de la longitud de una circunferencia

Como es lógico, habrás pensado hace un rato, que para calcular la longitud de una rueda, de un aro metálico, etc., no vamos a poner pintura en un punto de la rueda o del aro y hacer rodar hasta que nos haga una segunda señal en el suelo para después medir la distancia entre ambas señales.

Sería descabellado decir que con cortar el aro y enderezarlo ya podíamos medir su longitud.

La historia del cálculo de la longitud de una circunferencia tiene su historia, y muy larga por cierto. Casi 4 mil años ya comenzaron a darse cuenta algunos que se dedicaban al estudio de la naturaleza que algo raro pasaba entre el diámetro de una circunferencia y la periferia (de ahí el nombre de pi) o la curva o longitud de la circunferencia.

Hacían circunferencias con materiales blandos y de este modo medían, calculaban fácilmente sus longitudes. Dividían las longitudes de las diversas circunferencias y las dividían entre sus diámetros y siempre obtenían casi el mismo cociente.

Daba igual que la circunferencia tuviera un diámetro grande que uno pequeño, siempre obtenían casi el mismo resultado.

Hablamos de casi porque el número que resultaba de dividir la longitud de la circunferencia entre su diámetro no acababa nunca.

Las cifras decimales del cociente nunca se acaban.

Para que te des una idea, observa el valor de tal cociente con sus 200 primeras cifras decimales:

Como comprenderás, a este número había que darle un nombre para ahorrarnos complicaciones y pérdidas de tiempo, pues bien, por eso de periferia se le llamó PI y se le representa por la letra griega 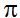 y se ha tomado la costumbre de utilizar para pequeños cálculos 4 decimales redondeando la cuarta cifra decimal  quedándonos el valor de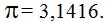 

Trabajando con circunferencias. Para que adquieras un buen conocimiento de la circunferencia y el cálculo de su longitud, sirviéndote de una regla y un compás vamos a hacer alguna pequeña práctica.

Dibuja una recta de 9 cm., que será el diámetro. Después, calcula la mitad de la misma y coloca la aguja del compás en ese punto, es decir, a 4,5 cm., del origen del diámetro y traza una semicircunferencia que pase por el origen y final del diámetro, tal como tienes en la figura:

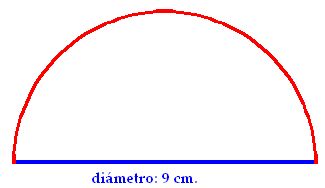
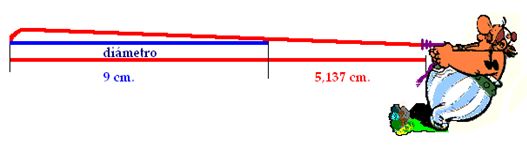
Si ahora estirásemos la semicircunferencia hasta ponerla recta la veríamos sobrepasando a la longitud del diámetro en algo más de 5,13 cm. Lo ves en la figura siguiente:

En la figura que tienes a continuación hemos dibujado algo así como una rueda girando y avanzando.

El radio de la rueda, es decir, la mitad del diámetro viene representado por una flecha roja. Al comienzo del movimiento de la rueda, la flecha señala el suelo.

A medida que la rueda avanza hacia la derecha la flecha va cambiando de posición.

Cuando la flecha coincida con el suelo por segunda vez querrá decir, que la rueda ha dado un giro completo o lo que es lo mismo, la rueda ha dado una vuelta completa y la medida entre estas dos posiciones de la flecha equivaldrá a la longitud de la rueda.

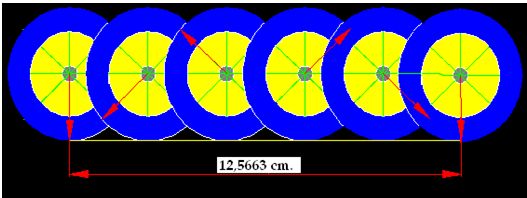
Observa que el diámetro de la rueda mide 4 cm., y la longitud de la rueda es de 12,5663 cm., (puedes comprobar con una regla graduada).

Si divides la longitud de la circunferencia entre el diámetro obtienes el valor de 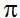 es decir, 3,1416 (no tenemos en cuenta el resto de las cifras decimales).

15.125  Observa la figura en la que el personaje Obélix estira la semicircunferencia. Comprobarás que el diámetro mide 9 cm., y la longitud de la semicircunferencia 14,137 cm. El cociente entre estas dos magnitudes ¿corresponderá con el valor de 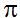? Razona la respuesta.

Respuesta: No, porque en este caso, estamos averiguando  la longitud de media circunferencia. El diámetro por 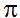equivale a la longitud de la circunferencia y en este caso sería: 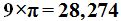Pero como se trata de la mitad de la circunferencia, el valor de ésta sería:  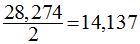cm., y si divides 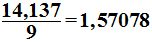que es exactamente, la mitad del valor de .

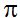15.126   Tienes tres ruedas de distintos tamaños que puedes ver en la siguiente figura:

¿Serán iguales los cocientes de dividir sus longitudes respectivas entre sus diámetros? Razona la respuesta.

Respuesta: Sí, sus cocientes valen 3,1416 porque no importan sus tamaños, sino el cociente de dividir  la longitud de cada una de ellas entre el valor de su  diámetro