Ecuaciones de Tercer, quinto, sexto ... Grado
Cabe preguntarse, después de aprender el modo de resolver las ecuaciones de 2º y 4º grados, siempre que en éstas no existan términos de grado 1 y 3, ¿cómo resolver las ecuaciones de grado tres, cinco, …?.
Cuando decimos que un polinomio, de cualquier grado, tiene raíces enteras o respuestas, significa al sustituirlas en el polinomio, el resultado nos da CERO.
Ejemplo:
¿Por qué?. Como la suma de las raíces o respuestas cambiada de signo debe darnos el coeficiente del término con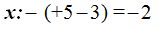 
Como puedes comprobar, el polinomio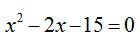 
hemos factorizado o puesto en forma de factores al decir que es igual a: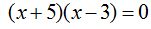 
13.67 Factoriza el polinomio: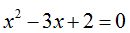 
Respuesta: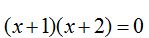 
13.68 Factoriza el polinomio: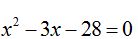 
Respuesta: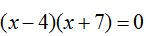 
13.69 Factoriza el polinomio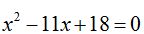 
Respuesta: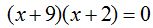 
En todos estos casos si sustituyes el valor de x, en cada una de las ecuaciones, por los valores hallados comprobarás que el resultado será igual a cero.
