Hallar el centro de giro de dos giros figuras honólogas
En la figura 22 tienes dos triángulos iguales. Sus lados homólogos son iguales. El problema que vamos a resolver es el modo de hallar el centro de giro pues vemos que para pasar de una posición a otra, hemos tenido que realizar una rotación cuyo centro es un punto exterior a las figuras
El circuncentro es el punto donde se encuentran las mediatrices, en nuestro caso, del triángulo.
Mediatriz de un segmento es la recta perpendicular a dicho segmento exactamente en su punto medio.
Analicemos paso como se determina el circuncentro:
En la figura 21 tienes un triángulo:
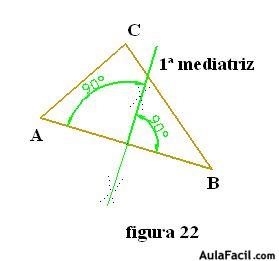
De este modo hemos calculado el punto medio del segmento AB y luego trazamos por ese punto una perpendicular (en verde). Así hemos determinado la primera mediatriz.
Hacemos lo mismo desde los puntos BC y CA en rojo y azul para determinar las otras dos mediatrices.
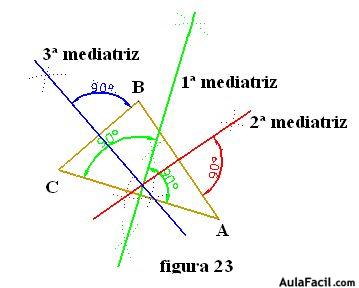
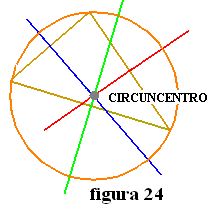
>El punto donde se cortan las tres mediatrices del triángulo se llama CIRCUNCENTRO.
En la figura 24 puedes ver la circunferencia que encierra o circunscribe al triángulo.
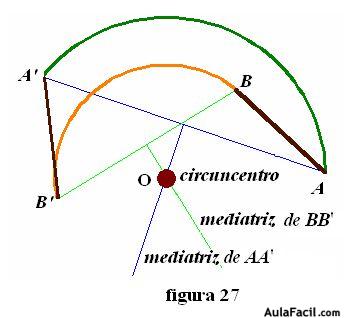
Vamos a determinar el centro de giro de dos segmentos homólogos.
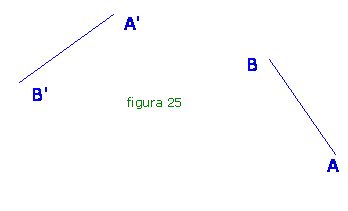
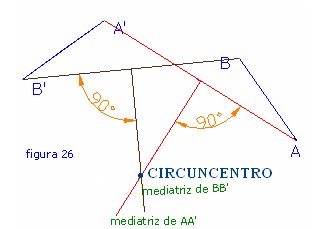
Comprobarás que las mediatrices de dos segmentos son dos rectas perpendiculares a los mismos en sus puntos medios. Los segmentos son AA’ y BB’