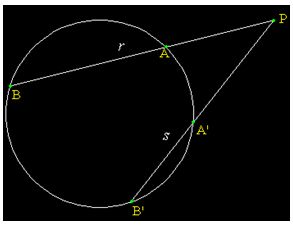
Potencia de un punto respecto de una circunferencia
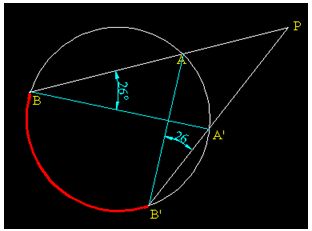
En la siguiente figura ves dos rectas r y s cuyo origen es P y son secantes a la circunferencia en A y B, y A’ yB’ respectivamente.
En geometría elemental estudiamos que el producto de las distancias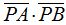 
y 
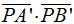son iguales porque los ángulos en B y B’ por abarcar el mismo arco (en color rojo) y ser el ángulo P común en los triángulos 
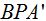y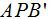 
tal como lo vemos en la siguiente figura:
Si el punto P es interior a la circunferencia:
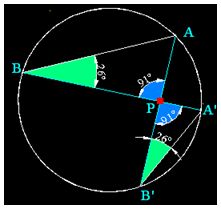
Los productos: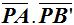 
y 
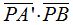son iguales en valores absolutos, porque si el sentido 
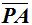consideramos positivo, 
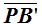será negativo y el producto también será negativo.
Si el punto es exterior a la circunferencia el resultado es positivo y si el punto es interior el resultado será negativo.
Puede darse el caso de que el punto corresponda a la circunferencia en este caso, el resultado será 0 como lo veremos más adelante.
La potencia del punto P se escribe, entre otras formas:
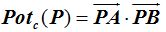
Ecuación analítica de la potencia de un punto respecto de una circunferencia
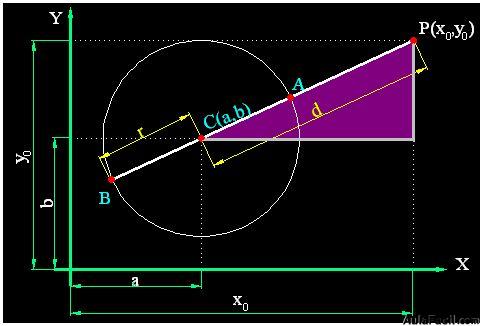
En la figura siguiente ves una circunferencia situada en el primer cuadrante de un eje de coordenadas con centro en C(a,b).
La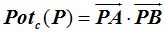 
podemos escribirla en función de los valores de la distancia d del punto 
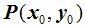al centro 
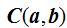y del radio r de la circunferencia:
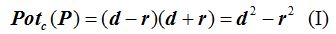
En el triángulo rectángulo, con fondo morado, ves que d es la hipotenusa cuyos catetos corresponden a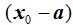 
y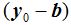 
respectivamente lo que nos permite escribir, siguiendo el teorema de Pitágoras:
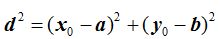
Este valor lo sustituimos en (I):
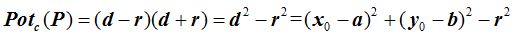
Tomando la ecuación de la circunferencia, comprobamos que para calcular la potencia de un punto respecto de una circunferencia, basta con sustituir las coordenadas del punto en su ecuación.
Observación:
Cuando el punto que consideramos pertenece a la circunferencia,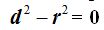 
26.5 Halla la potencia de un punto situado en (10,1) respecto a la circunferencia:
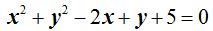
Respuesta: 87
Solución:
Sustituyes los valores de x e y, en la ecuación de la circunferencia por 10 y 1 respectivamente:
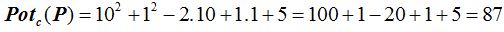
26.6 ¿Qué posición ocupan los puntos A(1,2) y B( 3,5) respecto a la circunferencia
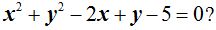
Respuesta: El 1º es un punto de la circunferencia
El 2º es un punto exterior a la circunferencia
Solución:
En ambos casos sustituimos valores:
1 )1+ 4 – 2 + 2 – 5 = 0 que significa que A(1,2) es un punto de la circunferencia.
2) 9 + 25 – 6 + 5 – 5 = 18 que significa que el punto es exterior a la circunferencia.
26.7 El punto A(10,1) ¿está en el interior de la circunferencia: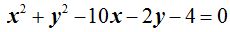 
?
Razona tu respuesta.
Respuesta: Sí, porque al sustituir valores, el resultado es negativo.
