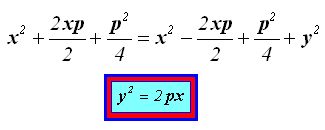Parábola
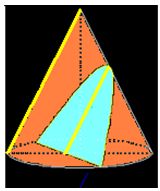
Cuando a un cono le das un corte paralelo a su generatriz obtienes una superficie o sección que la llamamos parábola:
También entendemos como parábola es el lugar geométrico de los puntos del plano que equidistan de un eje o recta (directriz) y de un punto al que llamamos foco.
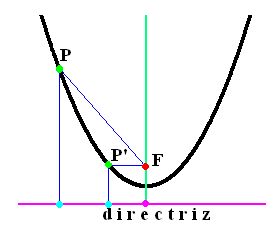
Nos fijamos en la figura siguiente:
Recordamos a la parábola de cuando estudiamos la ecuación de 2º grado.
Según lo que acabamos de definir, significa que la distancia desde cualquier punto P de la parábola al foco es la misma de la que hay entre el citado punto y una recta llamada directriz.
Construcción de una parábola
Un modo muy sencillo de construir una parábola con 4 clavos, dos listones de madera, una cuerda y un rotulador (puedes utilizar otras cosas) es el siguiente:
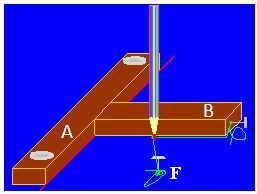
Sobre una hoja de papel trazas una línea, roja en la figura, y que hace las veces de la directriz.
Al listón A lo sujetas con dos clavos no sobrepasando la directriz (color rojo).
La cuerda (color verde) debe tener la longitud del listón B. Debes sujetarla en los clavos situados en el listónB y el que hace las veces del foco (F).
El rotulador, bolígrafo o lapicero situado sobre la superficie y mitad del hilo verde (bien tenso) debe estar pegado al listón B.
Haces deslizar con una mano el listón B al mismo tiempo que lo vas empujando con el lapicero o rotulador en contacto, éste, con la superficie, manteniendo tenso el hilo, comprobarás que sobre ella vas dibujando una parábola.
Elementos de una parábola
En la siguiente figura tienes numerados los elementos más importantes de la parábola:
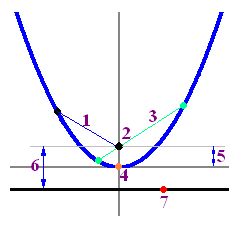
Los elementos señalados numéricamente corresponden a:
1.- Radio vector: une la distancia de un punto cualquiera de la parábola con el foco.
2.- Foco
3.- Cuerda focal: es el segmento que une la distancia de dos puntos de la parábola pasando por el foco.
4.- Vértice de la parábola: es el punto de intersección de la parábola con su eje principal.
5.- Semiparámetro: mitad de la distancia del foco a la directriz.
6.- Parámetro: distancia del foco a la directriz.
7.- Directriz: recta fija.
Nota.- Al parámetro y a la directriz se les designa con la letras p y d.
Excentricidad de la parábola
La excentricidad de la parábola nos viene dada por el cociente entre las distancias del foco a un punto y la que hay desde ese punto a la directriz.
Dado que ambas distancias son iguales, decimos que la excentricidad de una parábola vale 1.
Ecuación reducida o canónica de la parábola
En la parábola de la siguiente figura vemos que las distancias de un punto cualquiera de ella al foco y a la directriz son iguales.
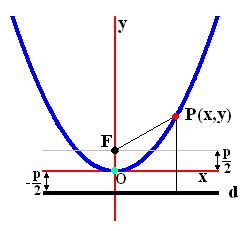
La distancia entre el punto P y la directriz será:
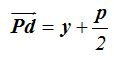
Vemos que las coordenadas del punto y del foco son:
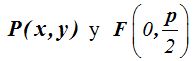respectivamente.
La distancia entre dos puntos teniendo en cuenta lo estudiado anteriormente (distancia entre dos puntos, distancia entre punto y recta, etc.):
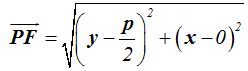
Como las distancias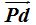 
y 
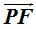son iguales, establecemos la igualdad:
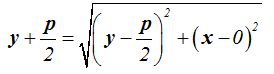
Elevando ambos miembros de la igualdad al cuadrado obtenemos:
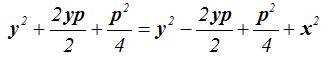
Reducimos términos semejantes:
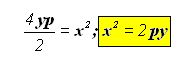
Acabas de aprender la ecuación de una parábola cuando su eje focal es vertical o paralelo al eje y.
En la figura siguiente tienes una parábola cuyo vértice se halla en el origen de coordenadas también pero su eje coincide con el eje de abscisas:
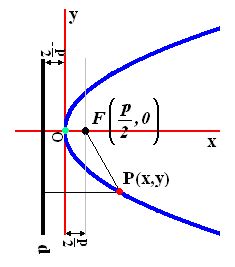
La distancia entre el punto P y la directriz será:
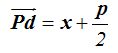
La distancia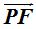 
podemos escribirla:
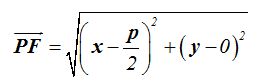
Como las distancias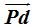 
y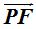 
son iguales, establecemos la igualdad:
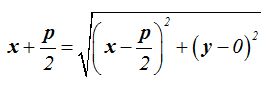
Elevando ambos miembros de la igualdad al cuadrado y reduciendo términos semejantes obtenemos:
