Parábola II
Resuelve los problemas siguientes:
(El programa Graphmatica que lo puedes descargar de forma gratuita, es muy práctico y sencillo para dibujar cónicas. Es el que utilizo en la resolución de los ejercicios siguentes).
26.34 Calcula las coordenadas del vértice, foco y ecuación de la directriz de la parábola:
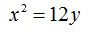
Dibújala.
Respuestas: V(0,0), F(0,3)
Ecuación de la directriz: y = - 3
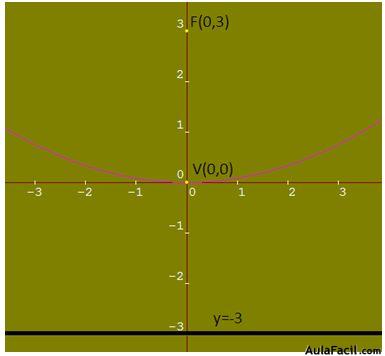
Solución
Vemos que: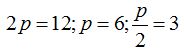 
El vértice de la parábola está a igual distancia del foco y de la directriz.
Las coordenadas del foco serán: (0,3).
La ecuación de la directriz: y = -3
26.35 Lo mismo que el problema anterior excepto que la ecuación de la parábola es:
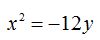
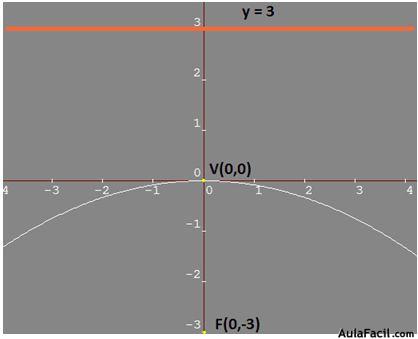
Respuestas: V(0,0), F(0,-3)
Ecuación de la directriz: y = 3
26.36 Calcula las coordenadas del vértice, foco y ecuación de la directriz de la parábola:
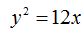
Dibújala.
Respuestas: V(0,0), F(3,0)
Ecuación de la directriz: x = - 3
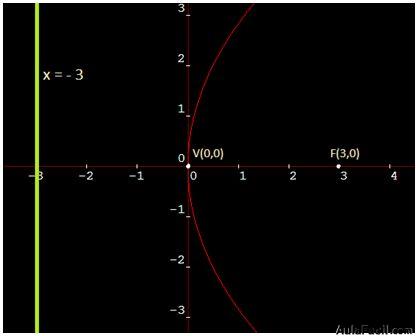
Solución
Vemos que:
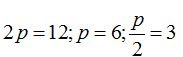
Las coordenadas del foco serán: (3,0).
La ecuación de la directriz: x = -3
26.37 Calcula lo pedido en el problema anterior pero teniendo en cuenta que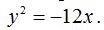 
Respuesta: V(0,0), F(-3,0); Ecuación de la directriz: x = 3
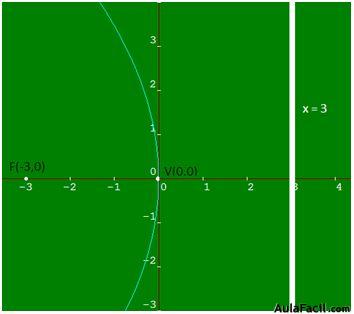
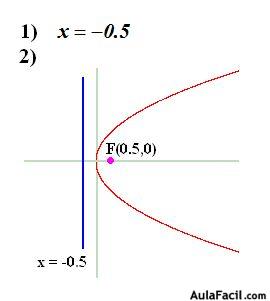
26.38 La ecuación de la directriz de una parábola es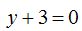 
y el foco se halla situado en el punto (0,3). Escribe la ecuación de esta parábola y dibújala.
el foco se halla situado en el punto (0,3). Escribe la ecuación de esta parábola y dibújala.
Respuestas: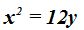 
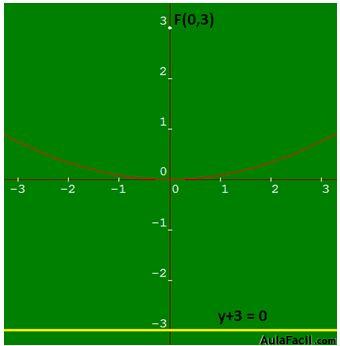
Solución
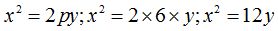
26.39 ¿Cuál es la ecuación de la parábola que tiene el vértice en el origen, por directriz la recta recta y + 4 = 0 y el foco se encuentra en el punto (0,4)?
Respuesta: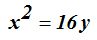 
Solución
El parámetro vale: 4 + 4 = 8. Aplicamos la fórmula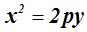 
(el eje focal es vertical) hallamos la respuesta.
26.40 Una parábola tiene como ecuación: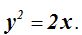 
Indica el valor de p y las coordenadas del foco.
Respuestas: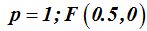 
Solución
Aplicando directamente la fórmula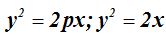 
vemos que: 
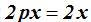, dividiendo ambos términos por 2x obtenemos p = 1.
Las coordenadas del foco que se halla en el eje de abscisas son:
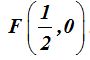
26.41 ¿Cuál es la ecuación de la directriz del problema anterior?
Dibuja la figura.
Respuestas:
