Hipérbola
Recordamos que si el plano corta a las generatrices en ambos lados del vértice del cono, obtenemos una hipérbola.
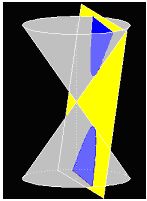
Las superficies comunes: plano y cono las podemos representar:
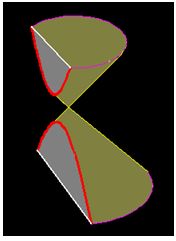
Las dos ramas de la hipérbola podemos trazarlas del siguiente modo:
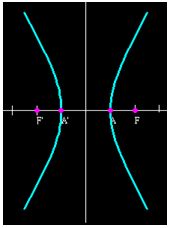
Esta hipérbola tiene su centro en el origen de coordenadas.
Los vértices están representados por A y A’ y los focos por F y F’.
La distancia entre los vértices nos viene dada por A’A = 2a
Hipérbola.- Definición
Hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos llamados focos se mantiene constante e igual a 2a.
Teniendo en cuenta la figura siguiente:
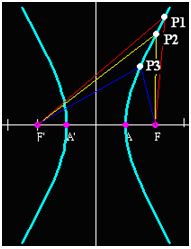
y sabiendo por el contenido de la definición comprobamos que las diferencias entre las distancias:
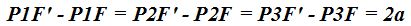
Construcción de una hipérbola
Hay varias formas sencillas para la construcción de hipérbolas. Describiremos dos:
A).- Necesitas tres pequeños clavos, un trozo de listón de madera (16 cm), una delgada cuerda (10 cm.) y chapa o tablero de madera.
Dos de los clavos los clavas, sin introducirlos del todo, en el tablero de madera (serían los FOCOS) separados 10 cm.
Las medidas pueden variar pero la distancia entre los focos debe ser mayor que la diferencia entre la longitud del listón y la de la cuerda. Longitud listón – longitud cuerda < F’F.

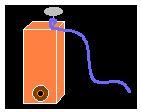
Al trozo de listón, que no tenga un grosor excesivo, que te sirva de regla, fijándote en la figura siguiente, le clavas el tercer clavo sin introducirlo del todo y le atas la cuerda.
En la parte posterior y a partir de la cara plana le haces un pequeño agujero tal como ves en la misma figura:
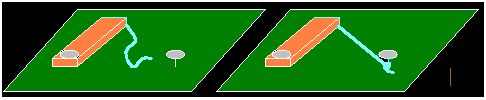
El trozo anterior de madera lo pones horizontal de modo que uno de los clavos de los focos pase por el agujero (lo habrás tenido que sacar e introducirlo nuevamente) y el extremo libre del cordel lo atas en el otro clavo libre que hace de foco.
Observa la figura siguiente tensando suavemente la cuerda (para ello tendrás poner un peso encima del trozo de madera o sujetarlo suavemente con una mano):
Colocas un lapicero, rotulador, etc., detrás de la cuerda que siempre has de mantenerla tensa:
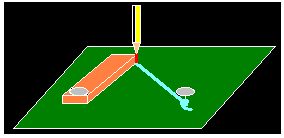
Ahora haces deslizar el rotulador, lapicero o bolígrafo tocando al trozo de madera y empujando a la cuerda manteniéndola un poco tensa (pisar con la mano suavemente a la madera o con un pequeño peso que le hayas puesto encima):
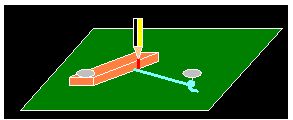
A medida que deslizas el lapicero o rotulador manteniendo tensa la cuerda irás dibujando sobre el color verde una rama de la hipérbola de color rojo, en el caso del ejemplo al tiempo que gira el trozo de madera.
Para completar la hipérbola te basta cambiar posiciones.
B).- Otro modo sencillo de trazar una hipérbola es el siguiente:
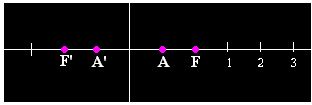
- Dibuja un eje de coordenadas
- Divide los ejes con divisiones de 1 cm y numéralos a partir del foco.
- Señala los focos y los vértices y te habrá quedado:
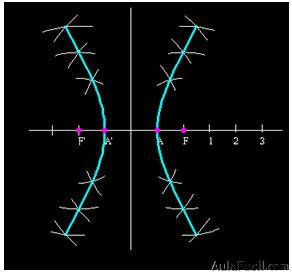
- Toma un compás, con radio igual a la distancia
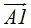 haciendo centro en F y F’ traza unos arcos (si quieres también circunferencias). Haces lo mismo pero con radios
haciendo centro en F y F’ traza unos arcos (si quieres también circunferencias). Haces lo mismo pero con radios 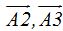 , etc , y uniendo los puntos creados por las intersecciones de los arcos obtenidos llegarás a:
, etc , y uniendo los puntos creados por las intersecciones de los arcos obtenidos llegarás a:
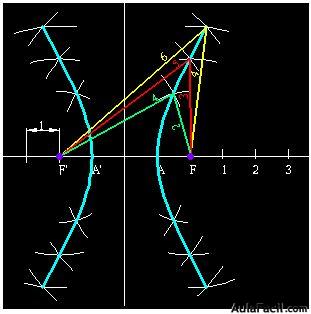
- Si hallas las distancias de un punto de la hipérbola a cada uno de los focos hallarás que sus diferencias valen lo mismo, una cantidad igual a 2a (distancia entre los vértices) en nuestro caso, 2 cm.
- Toma un compás, con radio igual a la distancia

