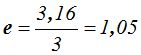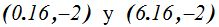Hipérbola III
Ecuación de la hipérbola vertical con centro en el origen de coordenadas
Hasta ahora hemos considerado eje principal de la hipérbola el paralelo al eje de abscisas.
En el caso de una hipérbola vertical con origen en el punto (0,0), su eje principal es el de ordenadas:
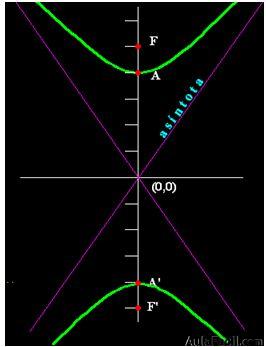
El centro de la hipérbola lo tenemos en el punto (0,0).
Los focos están situados en los puntos (0,5) y (0,-5).
Los vértices se encuentran en (0,4) y (0,-4).
Dado que los valores de x e y se han intercambiado, la ecuación de la hipérbola será:
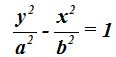
Si quieres obtener este resultado de un modo paso a paso, puedes comenzar en:
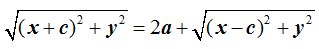de la demostración anterior.
Lo que tienes que hacer es cambiar x por y debido al giro de la figura:
A partir de aquí haces los cálculos del modo anterior y llegarás a la misma ecuación últimamente señalada.
Puedes servirte también cuanto a este tema nos referimos en la elipse teniendo en cuenta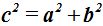 
Ecuación de la hipérbola vertical con centro fuera del origen de coordenadas
Si el centro de la hipérbola estuviese situado en el punto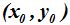 
la ecuación es:
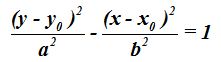
26.25 Sabemos que la medida del eje focal de una hipérbola mide 6 y la distancia entre los focos 10, ¿cuál es su ecuación?
Respuesta: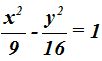 
Solución
Necesitamos conocer a y b
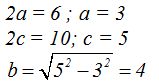
La ecuación será: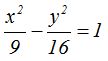 
26.26 Si la ecuación de una hipérbola es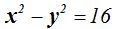 
escríbela en forma reducida o canónica.
Respuesta: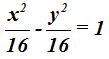 
26.27 Escribe la ecuación de una hipérbola de la que sabemos que su centro está en el origen de coordenadas, F(0,10) y A(0,6).
Respuesta: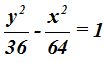 
Solución
Vemos que el eje principal es vertical.
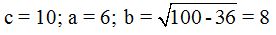
26.28 Si te dicen que la ecuación reducida o canónica de una hipérbola es:
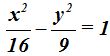
¿Cuáles son las coordenadas de los focos y vértices?
Respuesta: 
Excentricidad de la hipérbola
Hemos hecho referencia varias veces a la distancia focal y distancia entre vértices 2c y 2a ésta la menor de las dos, se llama excentricidad de la hipérbola al cociente entre ambas:
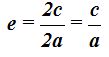
La excentricidad nos indica la abertura de las ramas de la hipérbola. A mayor excentricidad, mayor abertura.
La excentricidad de una hipérbola se mantiene con valor superior a 1, es decir,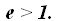 
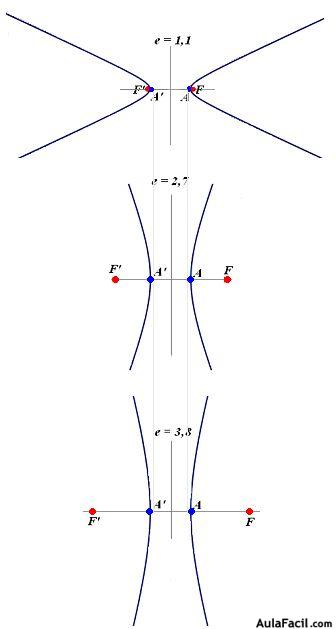
En la figura siguiente tienes las aberturas de las ramas de la hipérbola según sea el valor de la excentricidad.
Observa que las coordenadas de los vértices son iguales para cada una de las hipérbolas.
A medida que el valor de c aumenta, las ramas de la hipérbola tienden a hacerse más perpendiculares respecto al eje principal.
26,29 Calcula ecuación reducida o canónica, los vértices, los focos y la excentricidad de una hipérbola cuya ecuación general es:
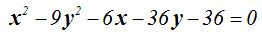
Respuestas: ecuación: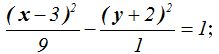 
Vértices :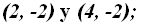 
Focos:
excentricidad: 1.05
Solución
La ecuación: podemos escribirla:
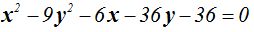
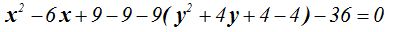
Haciendo operaciones y ordenando:
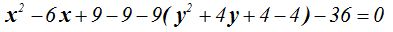
Reducimos términos semejantes:
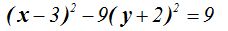
Dividimos todos los términos por 9:
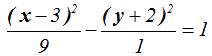
Observamos que el centro de esta hipérbola se halla en el punto (3,-2).
Los valores de a, b y c son:
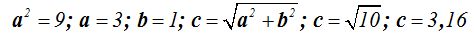
En la primera figura de las dos que tienes debajo y con los ejes de coordenadas cuyas líneas hechas con puntos fijamos el centro.
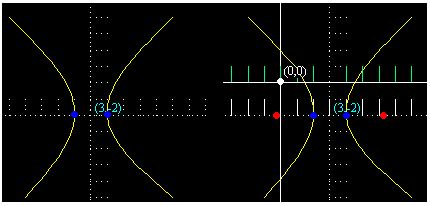
En la figura de la derecha con los ejes color blanco y línea continua, tienes el eje de coordenadas en el origen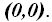 
En esta figura compruebas que los puntos que representan los vértices de la hipérbola, corresponden en el eje de las coordenadas en el origen, a los puntos (en azul):
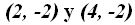y los focos (en rojo):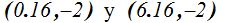 
La excentricidad vale : 
