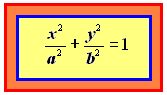Elipse
¿Qué entendemos por elipse?
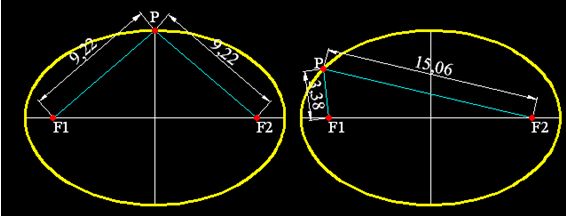
Se trata del lugar geométrico de los puntos (línea amarilla) cuya suma de distancias a dos puntos fijos F1 y F2llamados focos se mantiene constante:
Construcción de una elipse
A esta construcción se la conoce con el nombre de método del jardinero.
Puedes hacer con cartón liso, dos chinchetas, una cuerda y un bolígrafo. También puedes hacerla sobre arena sirviéndote de dos palos iguales, una cuerda y un tercer palo que acabe en punta para rayar el suelo.
La cuerda las atas a las chinchetas (amarillo clavadas en el cartón) o a los dos palos iguales (amarillo clavadas en la arena).
Con el bolígrafo o el palo acabado en punta y la cuerda tensada trazamos la línea que nos permite la cuerda:
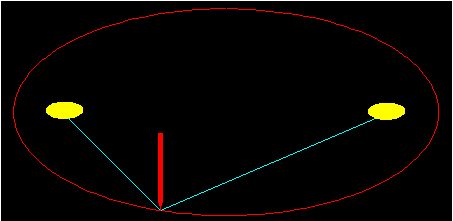
La figura obtenida será la elipse.
Elementos de una elipse
Vas a fijarte en la figura siguiente:
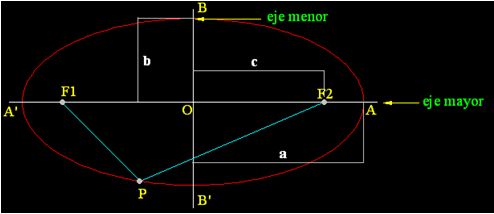
Diámetro mayor: 2a (AA’)
Diámetro menor: 2b (BB’)
Distancia focal (o entre focos):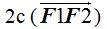 
Vértices de la elipse: A, A’, B, B’
Semieje menor: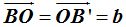 
Semieje mayor: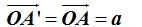 
En toda elipse según lo anterior, la suma de las distancias de un punto P a los focos se mantiene constante según puedes comprobar en la figura siguiente:
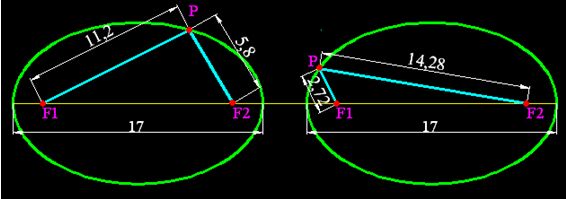
Según lo estudiado hasta aquí podemos escribir la igualdad:
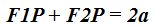
Elipses horizontales y verticales
Venimos estudiando la elipse horizontal que tiene el eje mayor (2a) en el eje de abscisas y el menor (2b) en el de ordenadas.
Cuando el eje mayor se encuentre en el de ordenadas y el menor en el de las abscisas decimos que se trata de una elipse vertical.
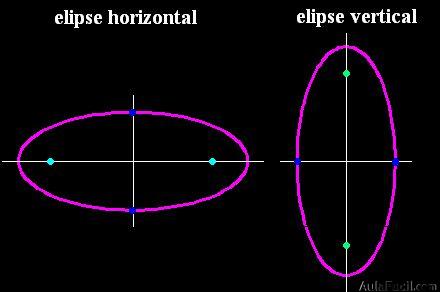
Es fácil saber si se trata horizontal y vertical. Lo sabemos desde el momento que nos den las coordenadas de los focos o vértices.
Si te dicen que los focos se encuentran en ( -3, 0) y (3, 0) vemos que se encuentra en el eje horizontal.
Se trata de una elipse horizontal.
Si los focos están situados en (0, -3) y (0, 3) significa que el eje mayor es vertical y horizontal el menor.
Se trata de una elipse vertical.
En ambos casos la suma de distancias de un punto de la elipse respecto a sus focos se mantiene constante (2a).
Ecuación reducida de la elipse
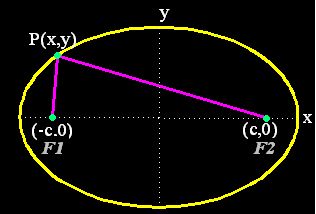
En la figura que tienes a continuación ves que el punto P(x,y) pertenece a la elipse.
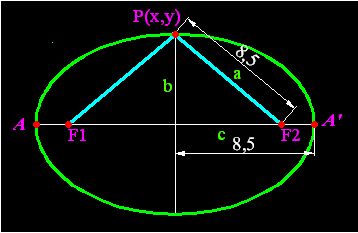
Teniendo en cuenta el teorema de Pitágoras podemos escribir:
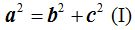
El punto F1 corresponde a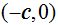 
y 
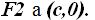
Tomando el punto P(x,y) en otro lugar de la elipse como lo tenemos a continuación y recordando la distancia entre dos puntos (en este caso no tenemos en cuenta el teorema de Pitágoras –no existe el ángulo recto-)podemos escribir:
La distancia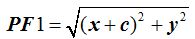 
La distancia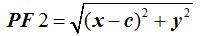 
La suma de ambas distancias es:
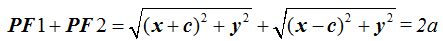
De esta igualdad vamos a obtener la fórmula de la elipse y para ello pasamos el segundo sumando a la derecha del signo (=):
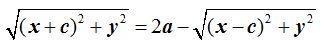
Elevamos ambos miembros al cuadrado:
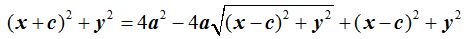
Después de reducir términos semejantes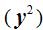 
, elevamos al cuadrado lo encerrado entre paréntesis excepto el radicando:
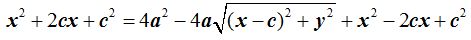
Reduciendo términos semejantes nos queda:
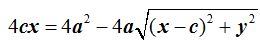simplificamos por 4 y llegamos a
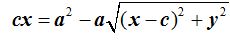
Elevamos ambos miembros al cuadrado después de dejar al término con la raíz cuadrada a la derecha del (=):
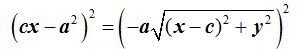
Haciendo operaciones:
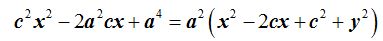
Quitando el paréntesis:
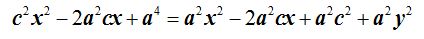
Reducimos términos semejantes:
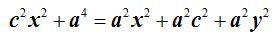
Dejamos a la izquierda del (=) a los términos que contienen incógnitas y sacamos factores comunes:
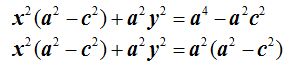
En (I) hemos deducido: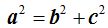 
. Obtenemos que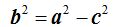 
Sustituimos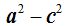 
por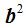 
:
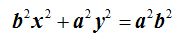
Dividimos por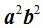 
a todos los términos:
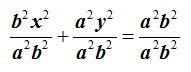
Simplificando llegamos a la ecuación reducida o canónica de la elipse con centro en el origen de coordenadas:
