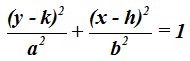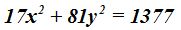Elipse II
26.14 Una elipse tiene sus focos situados en (-4, 0) y (4, 0). Sabemos que la suma de distancias desde estos puntos a un punto de la elipse es 9. Escribe la ecuación de la elipse.
Respuesta: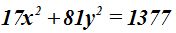 
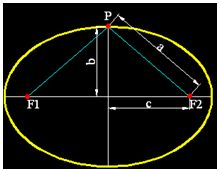
Datos que conocemos: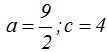 
Por Pitágoras según última figura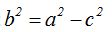 
Hacemos operaciones:
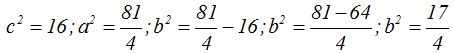
Tomamos de lo últimamente estudiado: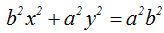 
y obtenemos:
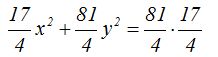
Simplificando denominadores:
26.14 Calcula las coordenadas de los focos y los vértices de la elipse cuya ecuación es:
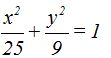
Respuestas: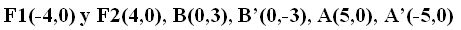 
Solución
Dibujamos la elipse con sus vértices:
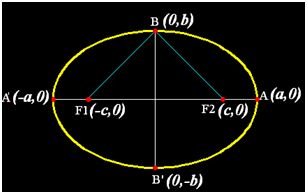
Del enunciado deducimos:
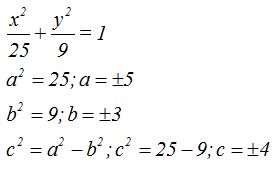
Ecuación de la elipse con centro fuera del origen de coordenadas
Hasta ahora hemos estudiado a la elipse cuando el centro se halla en (0,0) del eje de coordenadas, lo que conocemos como ecuación reducida o canónica de la elipse.
El centro de la elipse lo podemos tener situado en cualquier punto de los ejes de coordenadas.
En la siguiente figura hemos situado al centro de la elipse en el punto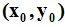 
.
Los nuevos valores de coordenadas quedan modificados cuya comprensión no te ofrecerán dificultades:
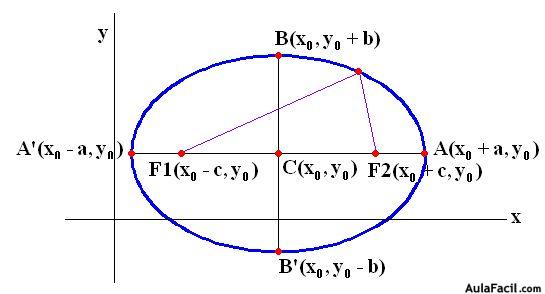
Otro modo de presentar la elipse con centro fuera del eje de coordenadas sería:
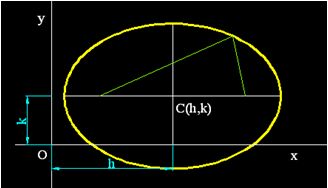
En este caso, el centro se halla en C(h,k) y la ecuación de la elipse será:
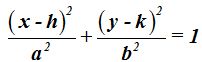
Cada vez que tengas que hallar la ecuación de una elipse con centro fuera del origen de coordenadas tendrás que transportarla al origen.
Veamos un ejemplo:
26.15 Una elipse con centro en el punto C(3,2), un foco en F(6,2) y A(8,2) ¿qué ecuación tiene?
Respuesta: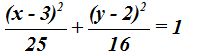 
Solución
La representamos gráficamente:
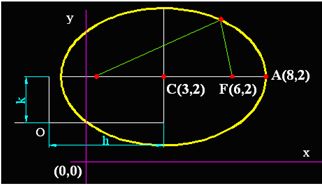
Distancia focal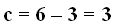 
semieje mayor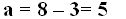 
semieje menor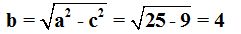 
Trasladamos el centro de esta elipse al origen de coordenadas y obtenemos:
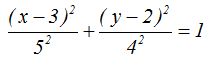
Ecuación general de la elipse
Hasta ahora no nos hemos referido a la ecuación general de la elipse.
Una ecuación como:
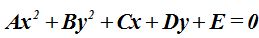
se refiere a la ecuación general de la elipse.
La obtenemos de un modo sencillo basándonos en la ecuación de la elipse con centro en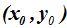 
y no en el origen de coordenadas.
Escribimos, según lo que acabas de estudiar, del modo siguiente:
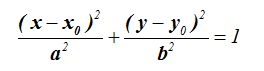
Haciendo operaciones tenemos:
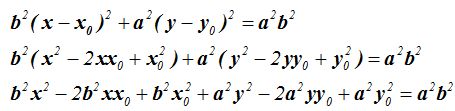
Ordenamos:
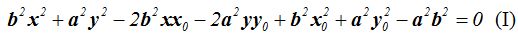
Damos los valores siguientes a:
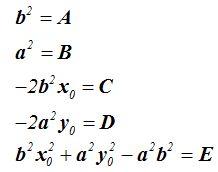
Sustituyendo en (I) obtenemos:
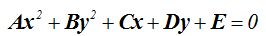
que es la ecuación general de la elipse.
Observa que los coeficientes de A y B tienen el mismo signo.
26.16 Sabemos que una elipse tiene su centro en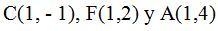 
¿Cuál es su ecuación?
Respuesta: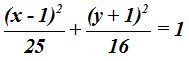 
26.17 La expresión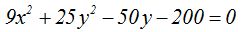 
¿se trata de la ecuación de una elipse?
Respuesta: Sí; la ecuación es: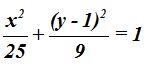 
Solución
Tienes que acomodarte a cada problema.
En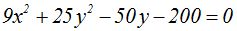 
podemos hacer las operaciones siguientes:
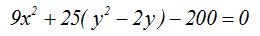
He sacado factor común a 25 en los términos que contienen y.
Para que sea el cuadrado de la diferencia de dos números observo que falta un 1: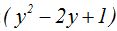 
. Si le añado 1 se lo tengo que restar para no alterar el valor de la expresión, pero, como el 1 está dentro del paréntesis, al multiplicar por 25, tengo que restar 25:
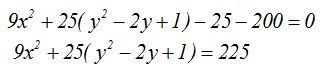
Haciendo operaciones:
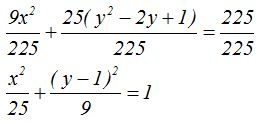
26.18 Se supone que la expresión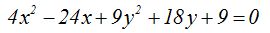 
expresa el valor de la ecuación de una elipse ¿podrías escribirla en su forma reducida o canónica?
Respuesta: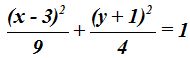 
Solución
Sacamos factores comunes
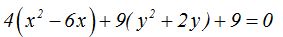
Sumamos al contenido de cada paréntesis un número que lo complete como cuadrado de la suma o diferencia de dos números y para que el valor no se altere, lo restamos multiplicado por el factor común correspondiente
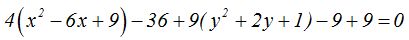
Al contenido de los paréntesis lo transformamos en productos notables y después, reducimos términos semejantes
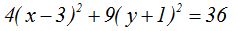
Dividimos todos los términos por 36
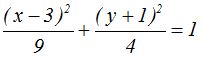
26.19 A partir de la igualdad: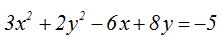 
la ecuación de la elipse.
Respuesta: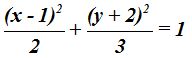 
Ecuación de la elipse vertical con centro en el origen de coordenadas
El eje principal que contiene las coordenadas de los focos y vértices del eje mayor es paralelo al eje de ordenadas.
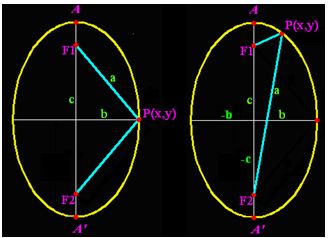
La suma de las distancias de un punto cualquiera de la elipse a los focos se mantiene constante e igual a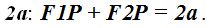 
Las coordenadas de los focos son: F1(0,c) y F2(0,-c).
Hacemos uso del cálculo de la distancia entre dos puntos:
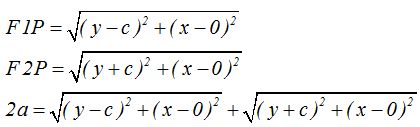
Pasamos la primera raíz a la izquierda del (=):
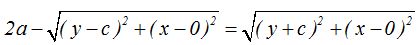
Elevamos ambos miembros al cuadrado y hacemos operaciones tal como tienes a continuación, paso a paso:
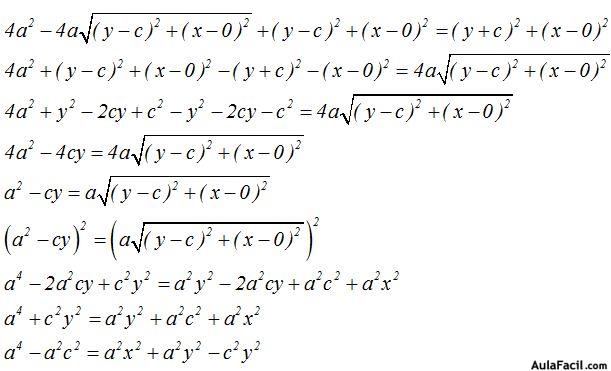
Sabemos que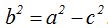 
Sacamos factores y sustituyendo 
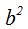por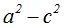 
tenemos:
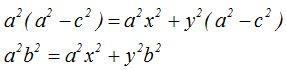
Dividiendo todos los términos por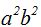 
simplificando y ordenando llegamos a:
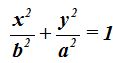, o bien,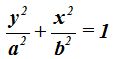 
Ecuación de la elipse vertical con centro fuera del origen de coordenadas
Suponiendo que el centro estuviese en C(h,k) la ecuación de la elipse vertical será:
