Centro Radical de tres Circunferencias II
26.12 Calcula la distancia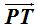 
de la figura siguiente que como ves, se trata de un segmento de la recta tangente.
Las coordenadas de P son (2,1).
La ecuación de la circunferencia es: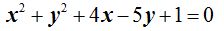 
Respuesta: 3 u.
Solución
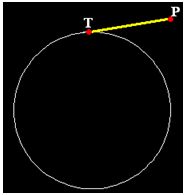
Se supone que el punto de tangencia es T.
Fíjate en la figura siguiente:
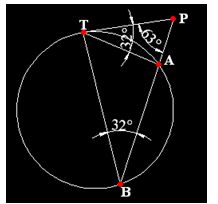
La potencia del punto P escribimos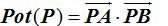 
En la última figura hemos colocado los puntos que nos interesan.
Se nos han formado dos triángulos: PTA y PBT que son semejantes. Compruébalos en las dos figuras siguientes:
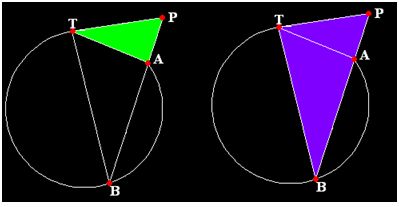
En el triángulo pequeño (verde), el ángulo en T es igual al ángulo en B del triángulo grande (morado) tal como ha quedado reflejado en la figura anterior a estas dos.
Por otra parte, el ángulo en P es el mismo para los dos triángulos. Esto quiere decir que son semejantes o que los lados son proporcionales:
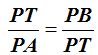
Producto de extremos igual al producto de medios:
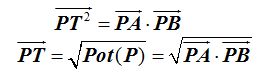
La longitud del segmento perteneciente a la tangente valdrá:
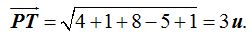
26.13 Sabemos que el radio de una circunferencia mide 4 unidades, que pasa por el punto (2,3) y el centro lo tiene situado en la recta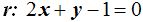 
.
¿Cuál es su ecuación?
Respuesta: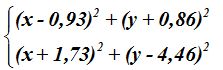 
Solución
Sirviéndonos de una figura anterior:
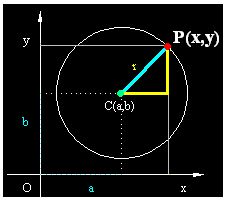
La distancia del centro a un punto de la circunferencia o radio, que la conocemos 4, podemos escribir:
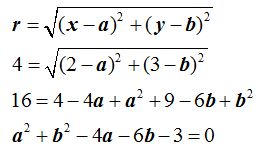
Si (a,b) son las coordenadas del centro y éste se halla en la recta:
2x+y-1= 0, la ecuación de esta recta podemos escribirla:
2a+b-1= 0
Resolvemos el sistema: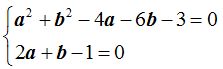 
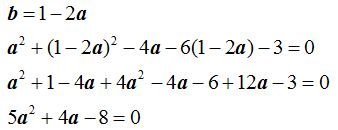
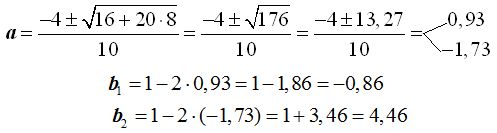
Tendremos dos circunferencias con centros en: (0.93,-0.86)
y
(-1.73,4.46)
cuyas ecuaciones son:
