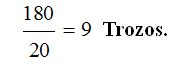Resolución de problemas de cuanto hemos estudiado del presente tema hasta aquí
3.61 Si tienes el número 15037 ¿Por qué cifras tienes que cambiar al cero y al 7 para que sea divisible por 3 y por 4 a la vez (divisible por 12).
Respuesta: Al 7 por 6 y al cero por 3.
Solución:
Para que un número sea divisible por 4, debe terminar en dos ceros o las dos últimas cifras han de ser divisibles por 4. Como 37 no es divisible por 4, pero sí 36 que se halla muy cerca. Basta con cambiar el 7 por el 6.
Me queda: 15036: Veo que la suma de sus cifras es múltiplo de 3:
1 + 5 + 0 + 3 + 6 = 15
Por tanto, este número es divisible por 3 y por 4.
Puedo cambiar al cero por 3, por, 6 ó 9 para que la suma de sus cifras siga dando un múltiplo de .
Podemos tener tres respuestas: 15336
15636
15936
Como todos estos números terminan en 36, serán múltiplos de 4 también.
3.62 Tres barras de acero de 360, 480 y 540 centímetros hemos dividido en trozos de igual longitud (la mayor posible). ¿Cuántos trozos hemos hecho y cuál es la longitud de cada uno?
Respuesta:
Solución:
Tendremos que calcular el mayor número que puesto en el divisor, divida a la longitud de cada barra un número exacto de veces, es decir, el m.c.d.(360, 480 y 540):
m.c.d.(360, 480 y 540) = 60
El total de metros que miden las 3 barras es: 360 + 480 + 540 = =1380
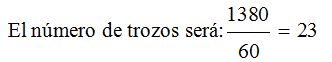
Respuesta: 60 metros cada trozo y 23 trozos en total
3.63 Al dividir a 38 y 43 por un cierto número se obtienen 2 y 3 como restos de las divisiones. ¿Cuál es el mayor divisor común para esos dos números que cumple con esta condición de dar 2 y como restos?
Respuesta: 4
Solución:
Si divides 12 entre 5 verás que la división no puede ser exacta. Te queda un resto, en este caso, el resto es 2.
Si al dividendo (12) le restas o le quitas el resto (2) el cociente es exacto. Si a 12 le quitas 2 te queda 10 y 10 es divisible entre 5.
Volvemos al problema:
Si a 38 le quitas 2: 38 – 2 = 36. Si a 36 le dividimos por ese número desconocido, la división es exacta y 36 es múltiplo de este divisor.
Si a 43 le quitas: 43 – 3 = 40. Si a 40 le dividimos por ese divisor desconocido, la división es exacta.
Ahora tienes que calcular el mayor divisor común a 40 y 36:
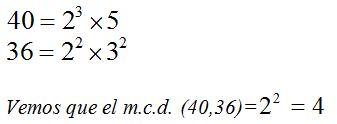
3.64 Si tienes tres barras de hierro que miden 40, 60 y 80 metros respectivamente y las divides en trozos de igual longitud, pero que ésta sea la mayor posible. ¿Cuántos trozos conseguirás y cuál será la longitud de cada trozo?
Respuesta: Cada trozo mide 20 metros
Número de trozos: 9.
Solución:
Tenemos que buscar un número, el más grande posible, que colocado como divisor, al hacer las divisiones de 40, 60 y 80 entre ese número, el resto sea cero.
Calculamos el máximo divisor que sea común a esos tres números:
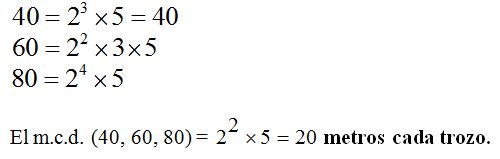
El mayor divisor común a 40, 60 y 80 es 20.
Cada trozo mide 20 metros. Para saber el número de trozos que podemos sacar, calculamos la longitud total de metros que tienen las tres barras: 40 + 60 + 80 = 180 metros.
Si cada trozo mide 20 metros, el número de trozos será: