Calcular todos los números Primos que hay entre los 209 primeros números naturales
Fue un matemático llamado Eratóstenes, nacido casi 300 años antes de Cristo quien ideó una forma sencilla para calcular los números primos.
CRIBA DE ERATÓSTENES:
Antes de comenzar, debes saber que, por criba se entiende un utensilio, generalmente una malla metálica que se usa para cribar o limpiar de impurezas el trigo u otras semillas.
La criba de Eratóstenes limpia de números compuestos y nos deja los números primos solamente.
Veamos lo vamos a hacer:
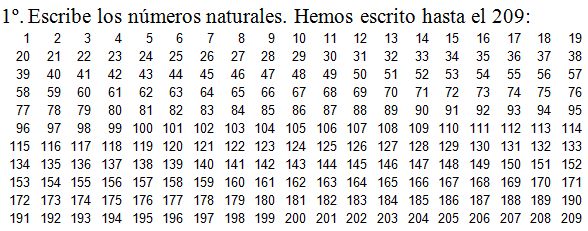
2º Multiplicamos 2 por sí mismo y nos da 4.
3º Nos colocamos sobre el 4, lo tachamos (en este ejemplo lo hemos pintado de rojo).
4º Contamos dos lugares a partir del 4 y nos encontramos con el 6 y hacemos lo mismo.
5º Seguimos contando 2 lugares y lo pintamos de rojo.
Todos los números en fondo rojo no son primos. Todos ellos tienen a 2 como divisor. En la primera pasada nos ha quedado:
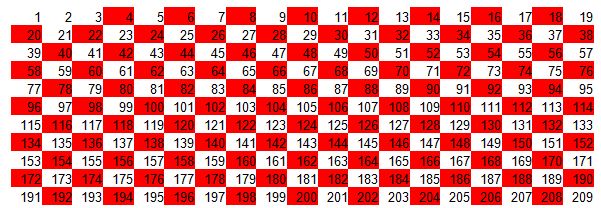
6º Ahora multiplica 3 por 3. Obtienes como resultado el 9, lo tachas y vas contando 3 lugares (SE CUENTAN LOS QUE TIENEN FONDO EN COLOR O SUPUESTAMENTE TACHADOS).
Los tachas, en nuestro caso lo hemos pintado de verde:
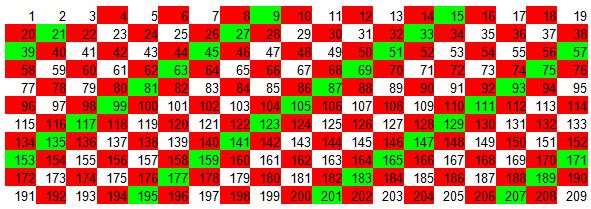
7º Ahora tomas el cinco lo multiplicas por sí mismo y obtienes 25.
Te colocas en 25, lo tachas, vas contando (incluyendo los tachados, en nuestro caso, los pintados) de 5 en 5 lugares. Los tachas (en nuestro caso lo pintamos de amarillo), si no está borrado o pintado, hasta terminar todos los números.
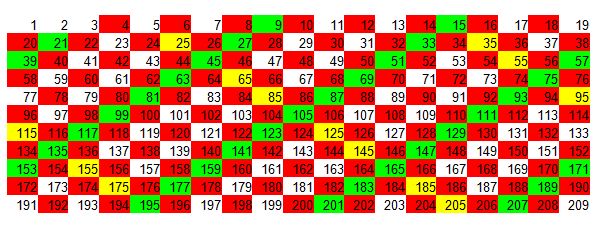
8º Multiplicas ahora 7 por sí mismo, te colocas en 49, lo tachamos o pintamos y a partir de este número vamos tachando, si no lo está, y pintamos de azul (contando siempre los tachados o pintados).
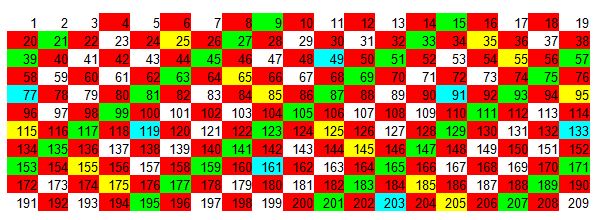
9º Tomamos el 11 y lo multiplicamos por sí mismo, nos situamos en 121, vamos contando de 11 en 11 y si no está pintado o tachado lo hacemos. Ahora utilizamos el color rosa claro.
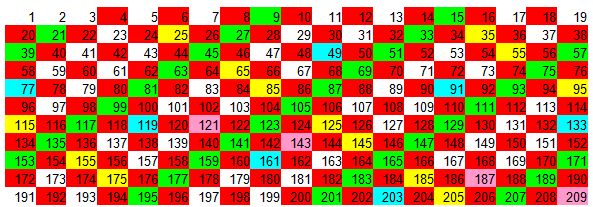
10 º Tomamos el 13 y lo multiplicamos por sí mismo y obtenemos 169. Nos situamos en 169, vamos contando de 13 en 13 y si no está pintado o tachado lo hacemos. Ahora utilizamos el color gris.
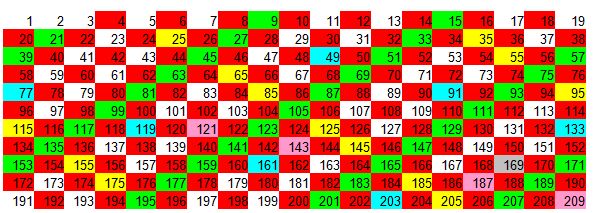
Como el siguiente número a 13 vemos que es 17. Al multiplicarlo por sí mismo nos pasamos de 209. Esto quiere decir que ya hemos terminado.
TODOS LOS NÚMEROS EN FONDO BLANCO SON PRIMOS.
3.17 Intenta hacer por tu cuenta una criba que deje pasar los 30 primeros números primos. Si tienes alguna duda no tienes más que consultar a lo que se te ha explicado.
MÚLTIPLOS Y DIVISORES:
Se dice que un número (12) es múltiplo de otro (4) cuando al dividir el primero entre el segundo, el resto es igual a cero:
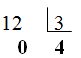
En este caso, 12 es múltiplo de 3.
Contesta a las preguntas siguientes:
3.17 ¿Es 12 múltiplo de 4?
3.18 ¿Es 36 múltiplo de 4?
3.19 ¿Es 45 múltiplo de 3?
3.20 ¿Es 55 múltiplo de 11?
3.21 ¿Es 63 múltiplo de 3?
3.22 ¿Es 122 múltiplo de 4?
3.23 ¿Es 217 múltiplo de 7?
3.24 ¿Es 100 múltiplo de 4?
3.25 ¿Es 76 múltiplo de 6?
Respuestas:
3.17 Sí. Al dividirlos obtenemos el resto cero.
3.18 Sí. Al dividirlos obtenemos el resto igual a cero.
3.19 Sí. Al dividirlos obtenemos el resto igual a cero.
3.20 Sí. Al dividirlos obtenemos el resto cero.
3.21 Sí. Al dividirlos obtenemos el resto igual a cero.
3.22 No. Al dividirlos no obtenemos el resto igual a cero.
3.23 Sí. Al dividirlos obtenemos el resto igual a cero.
3.24 Sí. Al dividirlos obtenemos el resto cero.
3.25 No. Al dividirlos no tenemos el resto igual a cero.
Se dice que un número es divisor de otro cuando lo divide exactamente.
Ejemplo: 3 divide exactamente a 9
5 no divide exactamente a 12
Podemos decir que 3 es un divisor de 9
y 5 no es un divisor de 12.
3.26 ¿Es 7 un divisor de 21?
3.27 ¿Es 5 un divisor de 127?
3.28 ¿Es 3 un divisor de 21?
3.29 ¿Es 11 un divisor de 121?
3.30 ¿Es 2 un divisor de 231?
3.31 ¿Es 4 un divisor de 1000?
3.32 ¿Es 3 un divisor de 213?
3.33 ¿Es 6 un divisor de 218?
3.34 ¿Es 7 un divisor de 210?
Respuestas:
3.26 21 contiene un número exacto de veces a 7. Sí, 7 es un divisor de 21.
3.27 127 no contiene un número exacto de veces a 5. No, 5 no es un divisor de 127.
3.28 21 contiene un número exacto de veces a 3. Sí, 3 es un divisor de 21.
3.29 121 contiene un número exacto de veces a 11. Sí, 11 es un divisor de 121.
3.30 231 no contiene un número exacto de veces a 2. No, 2 no es un divisor de 231.
3.31 1000 contiene un número exacto de veces a 4. Sí, 4 es un divisor de 1000.
3.32 213 contiene un número exacto de veces a 3. Sí, 3 es un divisor de 213.
3.33 218 no contiene un número exacto de veces a 6. No, 6 no es un divisor de 218.
3.34 210 contiene un número exacto de veces a 7. Sí, 7 es un divisor de 210.

