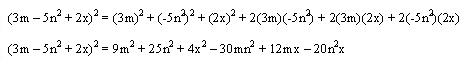Otros productos notables
Producto de la suma por la diferencia de dos cantidades.
Básicamente se escriben así:
(a + b)(a – b)
Si los multiplicamos queda:
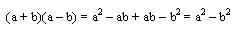
Entonces el producto notable es:
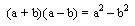
Se lee: la suma de dos cantidades multiplicada por su diferencia es igual a la diferencia de sus cuadrados.
Ejemplo:
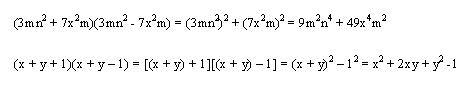
Como puede verse en el último ejemplo se puede convertir un polinomio de más de dos términos en un binomio con solo usar paréntesis y tomar lo que se encuentra en el paréntesis como un todo.
Producto de dos binomios que poseen un término común.
Tenemos los binomios (m + c)(m + b), donde “m” es el termino común, ahora desarrollamos la multiplicación.
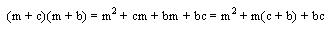
Como notable nos queda:
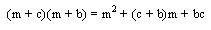
Se lee: El producto de dos binomios con un termino en común es igual al cuadrado de ese termino, más el producto de este por la suma algebraica de los otros dos, más el producto de estos.
Ejemplos:
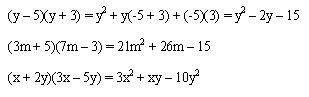
Cuadrado de un polinomio.
Desarrollemos un polinomio cualquiera al cuadrado:
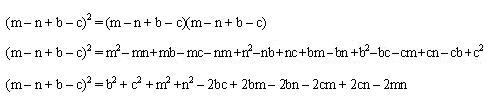
La ultima línea es el producto notable.
Observando el resultado ordenado podemos enunciarlo como producto notable:
El cuadrado de un polinomio es igual a la suma de los cuadrados de cada término, más el doble producto algebraico de cada uno de ellos por los demás.
Ejemplo: