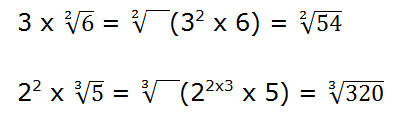Raíces
1.- Raíces
La raíz cuadrada de un número (A) es aquel número (B) que elevado al cuadrado nos da el primer número (A).
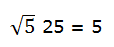
Ya que: 5 2 = 5 x 5 = 25
La raíz cúbica de un número (A) es aquel número (B) que elevado al cubo nos da el primer número (A).
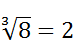
Por ejemplo:
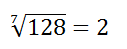
: Signo Radical
"n": Índice
“A”: Radicando
“B”: Raíz (cuadrada, cúbica, enésima...)
Vamos a distinguir cuando el radicando “A” es un número real positivo o negativo:
1.- Cuando el radicando es un número positivo hay que ver si el índice “n” es un número par o impar:
1.1.- Si “n” es un número “par” la raíz tiene dos soluciones: el mismo número con signo positivo y con signo negativo.
=5 (ya que: 5 2 = 5 x 5 = 25)
Pero también = -5 (ya que: -5 2 = -5 x -5 = 25)
1.2.- Si “n” es un número “impar” la raíz tiene una única solución que tiene signo positivo.
No puede existir una solución con signo negativo ya que al multiplicarla por sí mismo un número impar de veces el resultado siempre sería negativo.
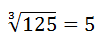
La solución no podría ser -5 ya que:
-5 x -5 x -5 = -125
2.- Cuando el radicando es un número negativo la raíz sólo tiene solución si el índice “n” es un número impar. Además la solución es única y es de signo negativo.
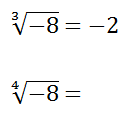No tiene solución
Ya que cualquier número negativo multiplicado por sí mismo un número “par” de veces el resultado es siempre positivo por lo que sería imposible obtener como resultado el radicando que tiene signo negativo.
-5 x -5 = 25
-5 x -5 x -5 x -5 = 625
2.- Raíz expresada como potencia
Cualquier raíz se puede expresar como potencia, siendo el exponente una fracción que tiene por numerador el exponente del radicando y por denominador el índice de la raíz.
=
3.- Extracción de factores en un radical
Para extraer un factor de un radical:
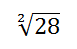
Comenzamos por descomponer factorialmente el radical:
28 = 22 x 7
Luego:
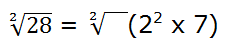
Sacamos de la raíz aquel factor cuyo exponente sea igual o múltiplo del índice de la raíz. En este ejemplo podemos sacar el factor 22.
Al sacar un factor fuera de la raíz su nuevo exponente será igual al exponente que tenía dentro de la raíz dividido por el índice de la raíz.
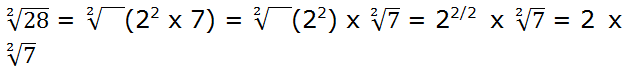
Cuando el exponente del factor no sea igual o múltiplo del índice de la raíz:
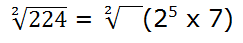
Actuamos de la siguiente manera:
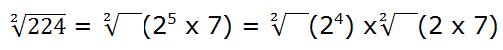
Hemos descompuesto 25 = 24 x 2 de manera que 24 tiene ya un exponente que es múltiplo del índice de la raíz y lo podemos extraer, mientras que el 2 lo dejamos dentro de la raíz.
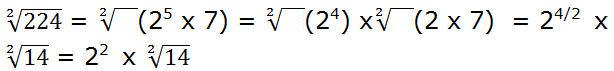
Veamos otro ejemplo:
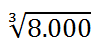
Descomponemos 8.000 = 26 x 53
Luego:
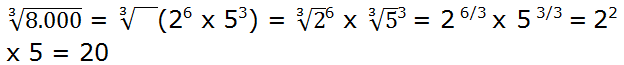
4.- Introducción de factores en un radical
Un número que esté multiplicando una raíz se puede introducir dentro de la raíz multiplicando su exponente por el índice de la raíz:
