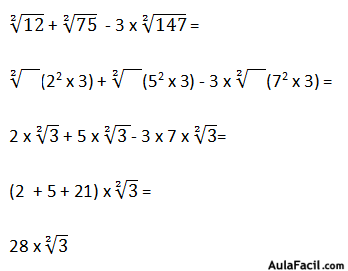Operaciones con raíces
a) Suma y resta de raíces
Se pueden sumar (restar) directamente aquellas raíces que tengan el mismo radicando y el mismo índice:
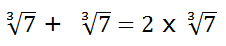
En aquellos casos en los que el índice de la raíz sí es igual pero los radicandos son diferentes hay que ver si es posible incluir o extraer algún factor para igualarlos:
Ejemplo:
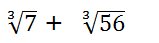
Descomponemos factorialmente 56 = 23 x 7
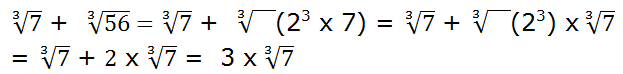
Otro ejemplo:
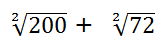
Descomponemos factorialmente 200 = 23 x 52 ; 72 = 23 x 32
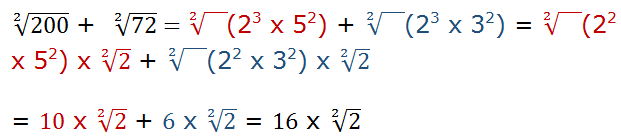
Si los índices de las raíces son diferentes o siendo iguales los radicandos son diferentes y no se pueden homogeneizar, entonces la suma (resta) se deja indicada o se resuelven las raíces y se suman sus soluciones.
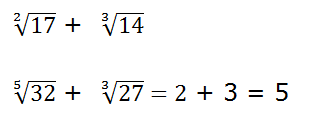
b) Multiplicación y división de raíces
Para multiplicar o dividir raíces deben de tener el mismo índice; de no ser así habría que transformar las raíces en otras semejantes (misma solución) que sí tuvieran el mismo índice.
b.1) Al multiplicar (dividir) raíces de igual índice se multiplican (dividen) los radicandos:
Ejemplos:
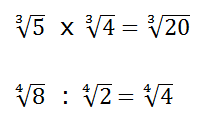
b.2) Raíces con distintos índices: buscamos raíces equivalentes con igual índice:
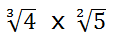
Para calcular una raíz equivalente a una dada se multiplica o divide el índice de la raíz y el exponente del radicando por el mismo número.
Empezamos calculando el mínimo común múltiplo de sus índices: m.c.m. = 3 x 2 = 6. Este va a ser el índice de las nuevas raíces:
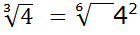( como el índice de la raíz (3) lo hemos multiplicado por 2 pasando a 6, el exponente del radicando (1) también lo multiplicamos por 2).
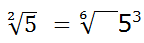(como el índice de la raíz (3) lo hemos multiplicado por 3, el exponente del radicando (1) también lo multiplicamos por 3).
Ahora ya podemos multiplicar:
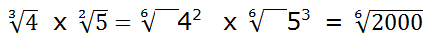
c) Eliminación de una raíz del denominador:
Cuando en una fracción tenemos una raíz en su denominador esto puede dificultar a la hora de operar por lo que puede resultar conveniente tratar de eliminar dicha raíz.
El método a utilizar puede depender de cada fracción; a continuación vamos a ver algunos ejemplos.
1er ejemplo:
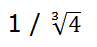
Vamos a multiplicar numerador y denominador por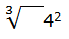 
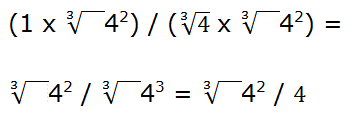
Hemos convertido una fracción con una raíz en el denominador en otra con la raíz en el numerador.
2º ejemplo:
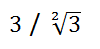
Vamos a multiplicar numerador y denominador por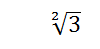 
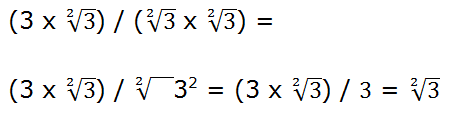
3er ejemplo:
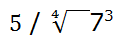
Vamos a multiplicar numerador y denominador por
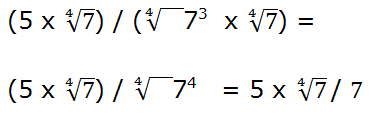
d) Potencia de una raíz:
Si una raíz se eleva a una potencia es igual que elevar el radicando a dicha potencia.
Ejemplos:
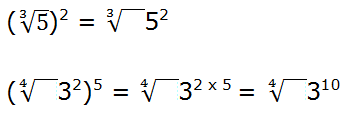
e) Raíz de una raíz:
La raíz de una raíz es una nueva raíz cuyo índice es el producto de los dos índices anteriores.
Ejemplos:
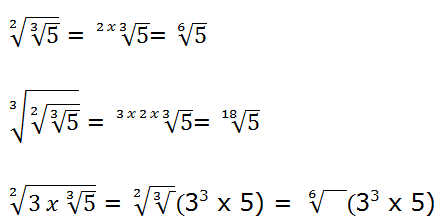(Hemos comenzado introduciendo el 3 dentro de la raíz interior)
f) Simplificación de expresiones combinadas:
Cuando tenemos una expresión con diversas raíces se puede ver la manera de simplificar la expresión.
Veamos un ejemplo:
