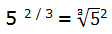Potencias de exponente entero
El exponente de una potencia puede ser un número entero y tener por tanto signo positivo o negativo.
Una potencia de signo negativo es igual a 1 dividido por la misma potencia con signo positivo:
X-n = 1 / Xn
Veamos un ejemplo:
4-3 = 1 / 43
1.- Propiedades de las potencias:
1.- El producto de 2 potencias con diferentes bases e iguales exponentes es igual al producto de sus bases manteniendo el mismo exponente.
33 x53 = 153
2.- La división de 2 potencias con diferentes bases e iguales exponente es igual a la división de sus bases manteniendo el mismo exponente.
122 :42 = 32
3.- El producto de 2 potencias con iguales bases y diferentes exponentes es igual a la misma base siendo su exponente la suma de los exponentes.
43 x45 = 43 + 5 = 48
4.- La división de 2 potencias con iguales bases y diferentes exponentes es igual a la misma base siendo su exponente la resta de los exponentes.
56 :54 = 56 - 4 = 52
5.- Una potencia elevada a otra potencia mantiene la misma base siendo el exponente el producto de sus exponentes.
( 52 )3 = 52 x 3 = 56
6.- Una fracción elevada a un exponente es igual a numerador y denominador elevados a dicho exponente.
( 2 / 6)3 = 23 / 63
7.- Una fracción elevada a un exponente negativo es igual a la fracción inversa elevada al exponente positivo.
( 2 / 6)-3 = ( 6 / 2)3
2.- Operaciones con potencias
A la hora de resolver operaciones combinadas el orden de resolución es el siguiente:
1.- Los paréntesis, comenzando por los paréntesis interiores
2.- Las potencias
3.- Las multiplicaciones y las divisiones
4.- Las sumas y las restas.
Veamos algunos ejemplos:
1º ejemplo:
(2 / 3)2 x (2 / 3)-2 =
(2 / 3)2 x (3 / 2)2 = (En rojo: la potencia negativa de una fracción es igual a la potencia positiva de la fracción inversa)
(2 / 3 x 3 / 2)2 = (En rojo: el producto de dos potencias de igual exponente es igual al producto de sus bases elevado a dicho exponente)
(6 / 6)2 = 1
2º ejemplo:
(42)3 – 46 =
46 – 46 = 0 (En rojo: una potencia elevada a otra potencia es igual a la base elevada al producto de sus exponentes)
3º ejemplo:
32 x 34 – (1 / 3)-6 =
32+4– (3 / 1)6 = (En rojo: el producto de dos potencias de la misma base es otra potencia de la misma base elevada a la suma de los exponentes; En azul: la potencia negativa de una fracción es igual a la potencia positiva de la fracción inversa)
36 – 36 = 0
4º ejemplo:
((5 / 7)2 - (7 / 4)-2)3 / (3 / 7)3 =
((5 / 7)2 - (4 / 7)2)3 / (3 / 7)3 = (En rojo: la potencia negativa de una fracción es igual a la potencia positiva de la fracción inversa)
(52 / 72 - 42 / 72)3 / (3 / 7)3 = (En rojo: la potencia de una fracción es igual a numerador y denominador elevados a dicha potencia)
((52 - 42) / 72)3 / (3 / 7)3 = (En rojo: restamos dos potencias de igual denominador)
(32 / 72)3 / (3 / 7)3 = (En rojo: simplificamos 52 - 42 = 9 = 32)
((32 x 7) / (72 x 3))3 = (En rojo: para dividir dos potencias de igual exponente se dividen las bases y se mantiene el mismo exponente)
(3 / 7)3 = 33 / 73
3.- Potencias con exponente racional
El exponente de una potencia puede ser una fracción:
5 2 / 3
Estas potencias son equivalentes a una raíz cuyo índice es el denominador de la fracción, siendo el radicando la base de la potencia y su exponente el numerador: