La recta real
Todos los números reales se pueden representar sobre la recta, cumpliéndose las siguientes propiedades:
a) A todo número real le corresponde un punto y sólo un punto sobre la recta.
b) A cada punto de la resta le corresponde un número real. No hay ningún punto de la recta graduada que no le corresponda un número real.
c) Nunca podremos decir que dos números reales son consecutivos porque entre ellos hay infinitos números reales.
Por ejemplo: 4,23 y 4,24 no son consecutivos porque entre ellos están por ejemplo los siguientes números:
4,23003, 4,231, 423222222, 4,230000000001….
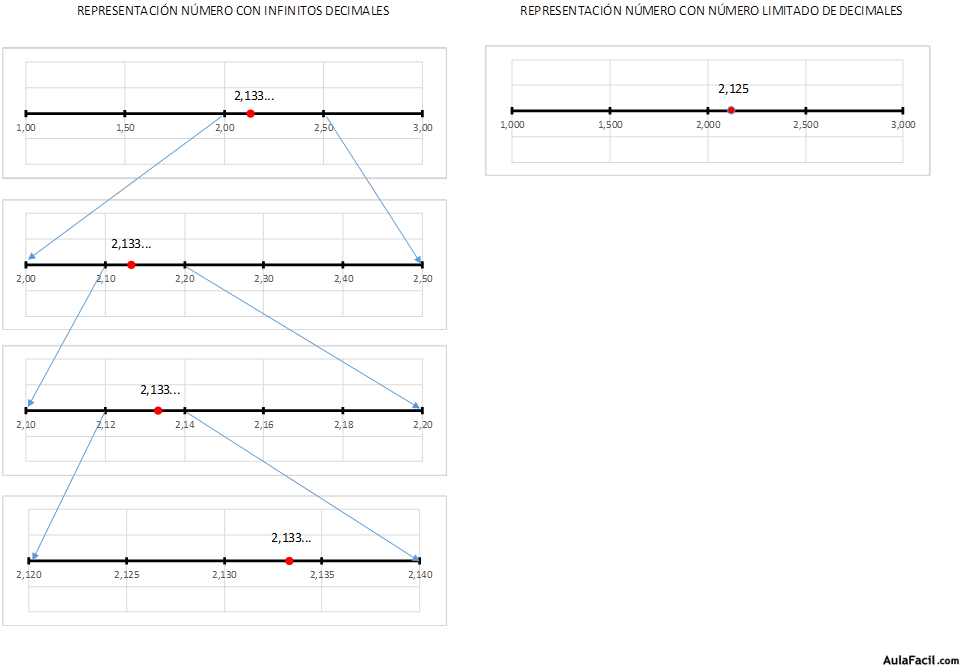
Para representar en la recta un número real hay que distinguir entre aquellos que tienen un número limitado de decimales, los cuales se pueden localizar en la recta con precisión.
Por ejemplo: 2,125
Y aquellos que tienen un número ilimitado de decimales, los cuales se pueden situar por aproximación.
Por ejemplo: 2,1333…
Podemos decidir con qué nivel de aproximación presentarlo:
1.- Intervalo de la recta real
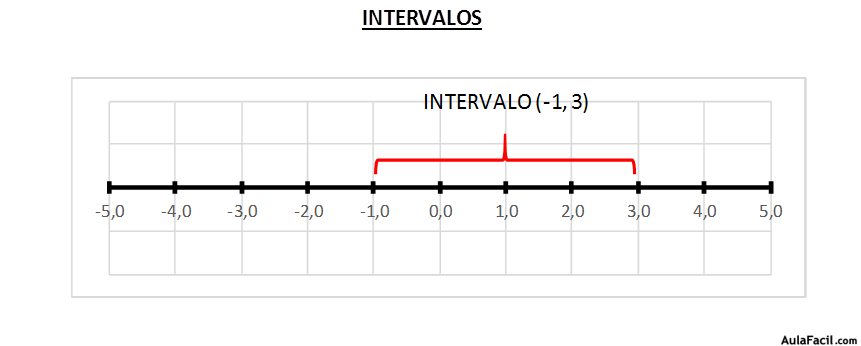
Un intervalo es un segmento de la recta real. Incluye a todos los número reales que hay entre dos límites establecidos denominados extremos del intervalo.
Por ejemplo, el segmento (-1, 3) incluye a los infinitos números reales que existen entre estos dos extremos
Los intervalos pueden ser:
a) Cerrados: cuando los extremos están incluidos dentro del mismo; se conoce por tanto en qué número real comienza el intervalo y en cuál termina. Se representan entre corchetes.
Por ejemplo: [-1, 3]
b) Abiertos: cuando los extremos no están incluidos dentro del mismo; no se conoce con exactitud en qué número real comienza y en cuál termina. Se representan entre paréntesis.
Por ejemplo: (-1, 3)
El -1 y el 3 no forman parte del intervalo. ¿Cuál es el primer número por la izquierda? -0,99, -0,999. -0,99999…. No se puede precisar.
c) Semiabierto o semicerrado: cuando está abierto por un extremo y cerrado por el otro.
Por ejemplo: (-1, 3]
Por ejemplo: [-1, 3)
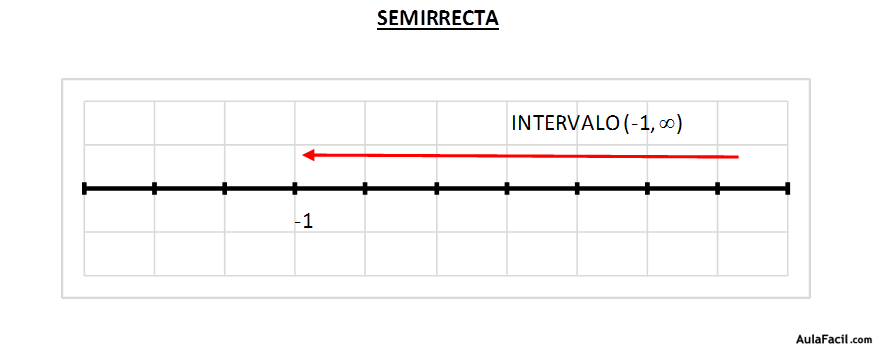
d) También puede ocurrir que el intervalo tan sólo tenga límite fijado en uno de los extremos y que el otro sea infinito.
Por ejemplo: (-1, ∞)
Por ejemplo: (∞, 3)
En este caso definiría una semirrecta de la recta real.
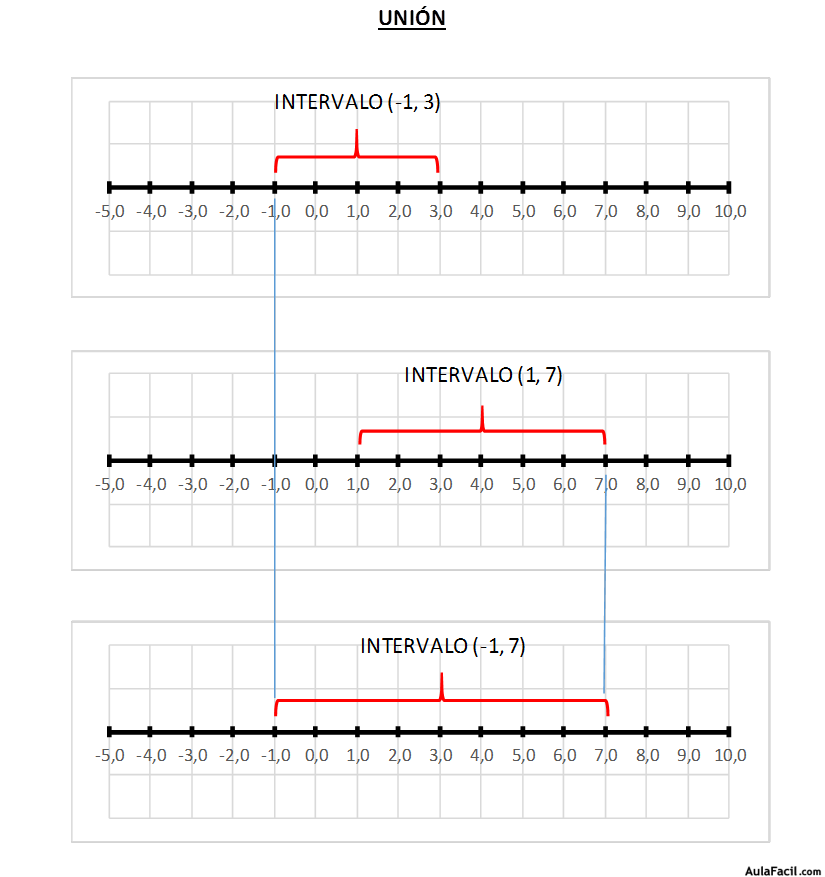
La unión de 2 intervalos se representa con el símbolo "U" y el intervalo resultante estaría formado por todos los números reales del primer intervalo y todos los números reales del segundo intervalo:
(-1, 3) U (1, 7) = (-1, 7)
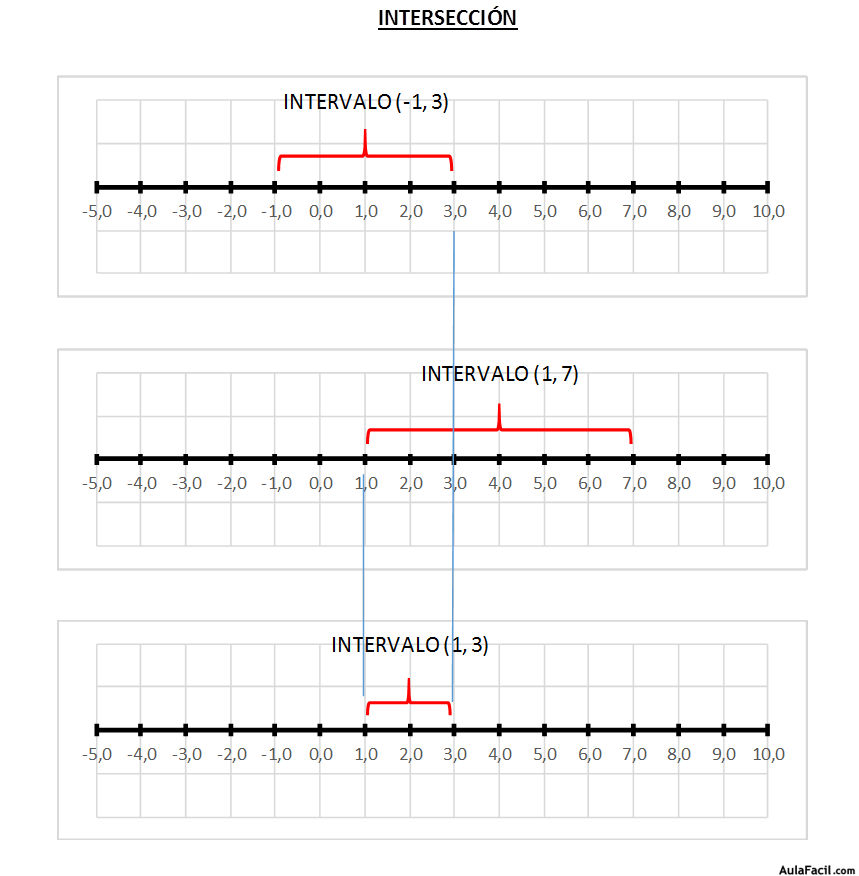
La intersección de 2 intervalos se representa con el símbolo “ ∩ “ y el intervalo resultante estaría formado por aquellos números reales comunes a ambos intervalos:
(-1, 3) ∩ (1, 7) = (1, 3)
Si los 2 intervalos no tuvieran puntos comunes su intersección sería el conjunto vacío:
(-1, 3) ∩ (5, 7) = O
La distancia (d) entre 2 puntos de la recta se calcula restando al número mayor el número menor.
Por ejemplo:
d (-1,72 , 4,55)
Restamos estos dos números: 4,55 – (-1,72) = 6,27
Por ejemplo:
d (-5,25 , -3,00)
Restamos estos dos números: -3,00 – (-5,25) = 2,25


