Posición relativa de rectas
1.- Rectas paralelas y rectas secantes
Dos rectas pueden ser paralelas (prolongándolas hasta el infinito nunca llegarían a cortarse) o secantes (prolongándolas hasta el infinito hay un punto en el que se cortan).
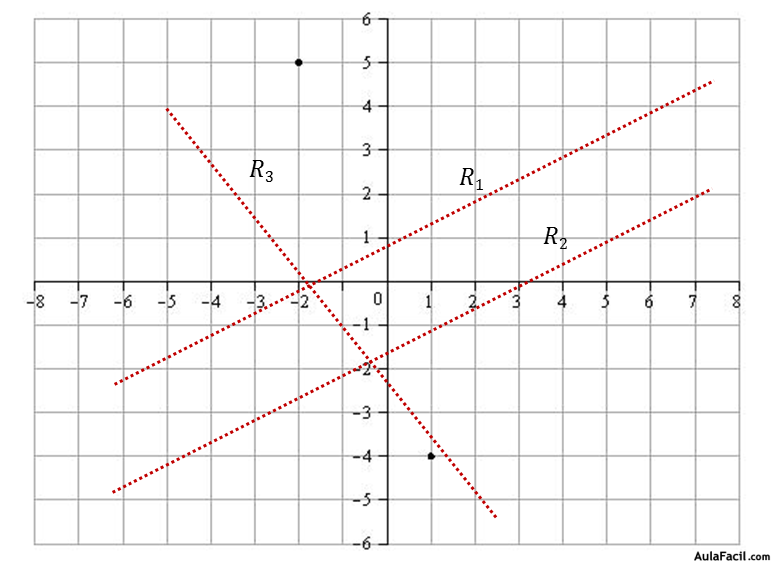
Las rectas R1 y R2 son paralelas mientras que la recta R3 es secante a las dos anteriores.
A partir de las ecuaciones de las rectas podemos saber si dos rectas son paralelas o secantes.
a) Ecuación general
La ecuación general de la recta:
A * X + B * Y + C = 0
Esta ecuación vimos que es la simplificación de la siguiente ecuación:
v2 * x - v1 * y - v2 * x1 + v1 * y1 = 0
Por lo que:
A = v2
B = -v1
Cuando desarrollamos esta ecuación vimos que V2 y V1 son las coordenadas de un vector paralelo a la recta.
También vimos antes que dos vectores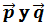 
son paralelos cuando sus coordenadas son proporcionales.
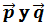son paralelos cuando sus coordenadas son proporcionales.
Luego, si dos rectas R1 (A * X + B * Y + C = 0) y R2 (A’ * X + B’ * Y + C’ = 0) son paralelas sus vectores directores también deben ser paralelos, por lo que se debe de cumplir que sus coordenadas sean proporcionales:
A / A’ = B / B’
Si no cumplen esta condición las rectas no son paralelas.
Veamos un ejemplo:
R1: 2X – 5Y + 3 = 0
R2: 4X – 10Y + 3 = 0
Vemos si cumplen la regla de paralelismo:
2 / 4 = -5 / -10 = 2
Luego estas dos reglas son paralelas.
Veamos otro ejemplo:
R1: 3X – 7Y + 3 = 0
R2: 2X – 5Y + 3 = 0
Vemos si cumplen la regla de paralelismo:
3 / 2 ≠ -7 / -5
Estas dos reglas no son paralelas, luego son secantes.
Si dos reglas paralelas cumples además:
A / A’ = B / B’ = C / C’
Entonces estas rectas no sólo son paralelas sino que son coincidentes (son la misma recta).
a.1) Cálculo del punto de corte de dos rectas secantes.
Hemos visto que:
R1: 3X – 7Y + 3 = 0
R2: 2X – 5Y + 3 = 0
Son rectas secantes.
Para calcular el punto de corte despejamos X en la primera ecuación:
X = (7Y – 3) / 3
Y sustituimos su valor en la segunda ecuación:
2X – 5Y + 3 = 0
2 * (7Y – 3) / 3 – 5Y + 3 = 0
14Y – 6 – 15Y + 9 = 0
-Y = -3 (Luego Y = 3)
Calculamos ahora el valor de X.
X = (7*3 – 3) / 3 = 6
Por lo tanto el punto de corte de ambas rectas es p1 (6, 3)
b) Ecuación explícita
La ecuación explícita de la recta:
Y = T * X + n
Dos rectas son paralelas cuando tienen la misma pendiente.
Luego, dos rectas R1 (Y = T * X + n) y R2 (Y = T’ * X + n’) son paralelas cuando cumplen:
T = T’
Veamos un ejemplo:
R1: Y = 0,3 * X + 2
R2: Y = 0,3 * X - 5
Vemos que estas dos rectas cumplen:
T = T’ = 0,3
Por lo que son paralelas.
b.1) Cálculo del punto de corte de dos rectas secantes
Tomamos 2 rectas secantes
R1: Y = 0,7 * X - 4
R2: Y = 0,2 * X - 4
Para calcular el punto de corte despejamos en la primera ecuación X:
X = (Y + 4) / 0,7
Y sustituimos su valor en la segunda ecuación:
Y = 0,2 * X - 4
Y = 0,2 * (Y + 4) / 0,7 - 4
0,7Y = 0,2Y + 0,8 – 2,8
0,5Y = -2 (Luego Y = -4)
Calculamos ahora el valor de X.
X = (-4 + 4) / 0,7 =0
Por lo tanto el punto de corte de ambas rectas es p1 (0, -4)
