Pendiente de una recta
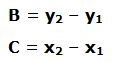
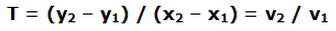
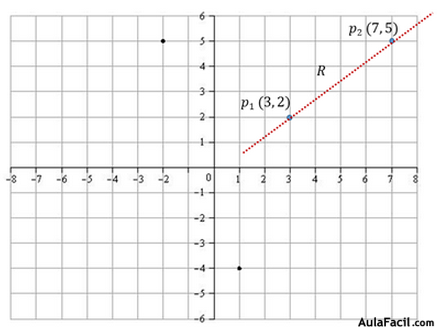
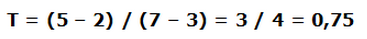
2.- Pendiente y tangente
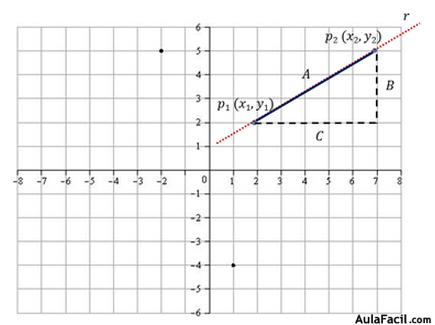
Vimos en trigonometría que la tangente de un ángulo α es igual al cateto opuesto al ángulo dividido por el cateto contiguo al ángulo.
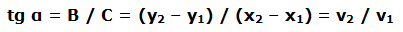
Vemos por tanto que la tg α coincide con la definición de la pendiente de la recta R.
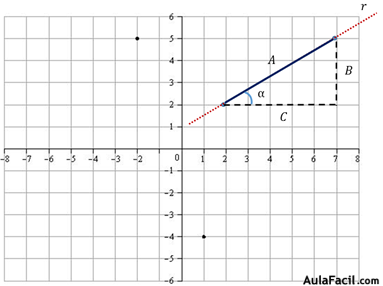
Este ángulo α es exactamente igual que el ángulo que forma la recta R al cortar el eje de abscisa.
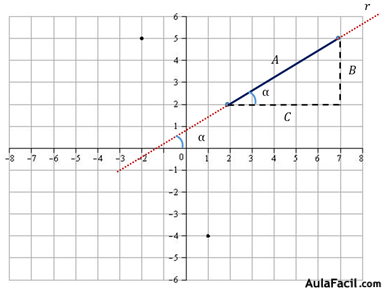
Por lo que la pendiente de una recta es igual a la tangente del ángulo que forma dicha recta al cortar el eje de abscisas.
Vimos también en trigonometría el signo de la tangente (y por lo tanto de la pendiente de la recta):
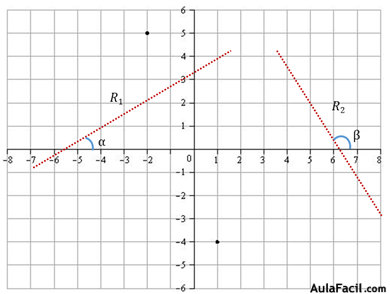
· Si el ángulo α se sitúa entre 0º y 90º la pendiente de la recta es positiva
· Si el ángulo α se sitúa entre 90º y 180º la pendiente de la recta es negativa
La recta R1 del siguiente gráfico tiene pendiente positiva (su ángulo es se sitúa entre 0º y 90º), mientras que la recta R2 tiene pendiente negativa (su ángulo se sitúa entre 90º y 180º).
3.- Ecuación explicita de la recta
En el desarrollo de la ecuación general de la recta vimos:
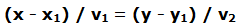
Operando:
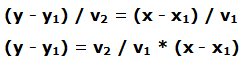
Hemos visto que v2 / v1 es la pendiente de la recta y es igual a la tangente “T” del ángulo que forma la recta al cortar el eje de abscisas.
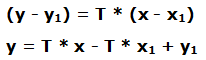
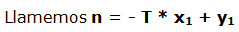
La ecuación queda definida:
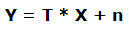
Veamos un ejemplo:
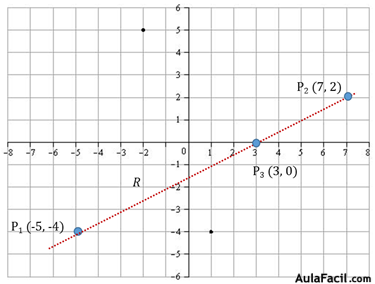
La recta R pasa por los puntos p1 (x1, y1) y p2 (x2, y2) cuyas coordenadas son (-5, -4) y (7, 2) respectivamente.
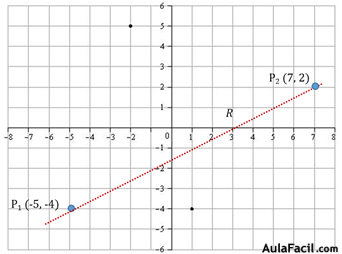
Calculamos su pendiente:

ATENCIÓN: El valor “n” (-1,5) es el valor que toma Y cuando X = 0, y coincide con el punto de corte de la recta con el eje de coordenada.
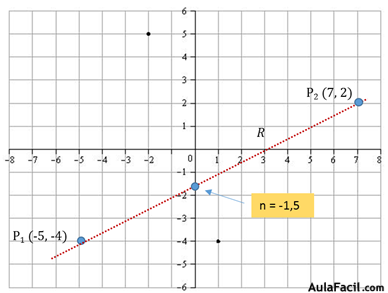
Vamos a calcular un nuevo punto p3:
Si x = 3
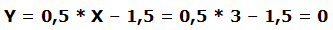
Las coordenadas de este punto serían p3 (3, 0)