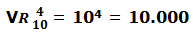Combinatoria: Variaciones
1.- Variaciones
Se denominan variaciones al número de grupos diferentes de “n” elementos que se pueden formar a partir de un grupo inicial de “m” elementos.
Una nota característica de las variaciones es que el orden importa.
Por ejemplo, si a partir de las 5 vocales formamos grupos de 3 vocales, el grupo “A – E – I” es diferente del grupo “A – I – E” ya que el orden de las vocales es diferente.
Dentro de las variaciones distinguimos:
a) Variaciones sin repetición
En las variaciones sin repetición, también denominadas variaciones ordinarias, ningún elemento del grupo inicial se puede repetir.
Por ejemplo, si a partir de las 5 vocales formamos grupos de 3 vocales, el grupo “A – A – I” no valdría ya que se repite la vocal “A”.
En las variaciones sin repetición se tiene que cumplir que n <= m.
Es decir, con las 5 vocales (m) no podemos formar grupos de 6 vocales (n) ya que al menos una se tendría que repetir.
Las variaciones sin repetición se representan por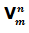 
o también por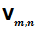 
Por ejemplo: Tenemos las 5 vocales y quiero ver cuantos grupos de 3 vocales podemos formar:
A – E – I
E – O - U
I – U – A
Para calcular el número de grupos que se puede formar se aplica la fórmula.
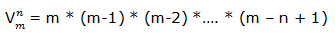
Siendo:
m : número total de elementos
n : tamaño de los grupos
En el ejemplo anterior la fórmula aplicada sería:
Se podrían formar hasta 60 grupos diferentes de 3 vocales.
Las variaciones sin repetición también se pueden calcular utilizando factoriales.
El factorial de un número “n” se representa por n! y se calcula:
n! = n * (n-1) * (n-2) * …* 3 * 2 * 1
Veamos un ejemplo:
6! = 6 * 5 * 4 * 3 * 2 * 1 = 720
Las variaciones sin repetición utilizando factoriales se calculan:
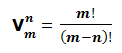
En nuestro ejemplo sería:
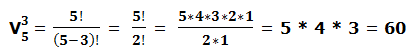
Veamos otros ejemplos:
En una clase de 20 alumnos se organiza un campeonato de ajedrez y se premia a los 5 primeros; ¿Cuántos resultados diferentes pueden darse?
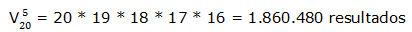
En este ejemplo el orden importa: no es lo mismo quedar 1º que 3º.
En un club se celebran elecciones para elegir presidente, 1er vocal y 2 vocal entre 40 candidatos; ¿Cuántos resultados diferentes pueden darse?
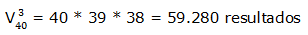
En una carrera de caballos con 15 participantes haces una apuesta triple (acertar caballo ganador, 2º y 3er clasificado); ¿Cuántos resultados diferentes pueden darse?
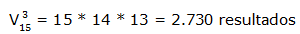
b) Variaciones con repetición
En las variaciones con sí se puede repetir una o varias veces un mismo elemento.
Por ejemplo, si a partir de las 5 vocales formamos grupos de 3 vocales, el grupo “A – A – I” sí valdría.
E grupo “A – A – A” también valdría.
En las variaciones con repetición es posible que n > m.
Es decir, con las 5 vocales (m) podemos formar grupos de 8 vocales (n):
“A – E – A – I – O – E – U - A”
Las variaciones con repetición se representan por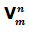 
El orden sigue siendo relevante:
A – A – I
A – I - A
Cuentan como 2 grupos diferentes.
Para calcular el número de grupos que se pueden formar se aplica la fórmula.
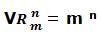
Siendo:
m : número total de elementos
n : tamaño de los grupos
En el ejemplo de cuantos grupos de 3 vocales se pueden formar con las 5 vocales el resultado sería:
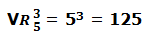
Veamos algunos ejemplos:
En una quiniela de 14 apuestas (1 = gana; X = empata; 2 = pierde) cuantos resultados diferentes pueden darse.
Aplicamos la fórmula de variaciones con repetición ya que las 3 opciones (1 – X – 2) se pueden repetir hasta 14 veces.
m = 3 (1 – X – 2)
n = 14 (cada quiniela tiene 14 partidos)
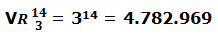
En una bolsa hay 5 números (del 1 al 5) y hacemos 6 extracciones (cada vez que sacamos un número lo volvemos a meter en la bolsa por lo que se puede repetir); ¿Cuántos resultados pueden darse?
m = 5 (números del 1 al 5)
n = 6 (cada resultado está formado por 6 extracciones)
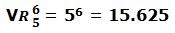
En una clase de 20 alumnos se entregan 3 premios (música, deporte y arte); un mismo alumno puede repetir premio. ¿Cuantos posibles resultados pueden darse?
m = 20 (nº de alumnos de la clase)
n = 3 (cada posible resultado está formado por 3 premiados)
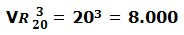
¿Cuántos números diferentes se pueden formar con las 10 cifras (del 0 al 9) agrupadas de 4 en 4, pudiéndose repetir las cifras.
m = 10 (nº de cifras diferentes)
n = 4 (los números que queremos formar tienen 4 cifras)
