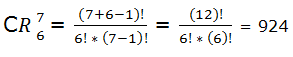Combinaciones
1.- Combinaciones
Se denominan combinaciones al número de grupos diferentes de “n” elementos que se pueden formar a partir de un grupo inicial de “m” elementos.
Una nota característica de las combinaciones, y que les diferencia de las variaciones, es que el orden no importa.
Por ejemplo, si a partir de las 5 vocales formamos grupos de 3 vocales, el grupo “A – E – I” es igual que el grupo “A – I – E” por lo que tan sólo computan 1 vez.
Dentro de las combinaciones distinguimos:
a) Combinaciones sin repetición
En las combinaciones sin repetición, como su propio nombre indica, ningún elemento se puede repetir.
Obligatoriamente n <= m.
Las combinaciones sin repetición se representan por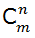 
o también por 
.
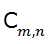Para calcular el número de grupos que se pueden formar se aplica la fórmula.
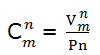
Es decir, las combinaciones de m elementos tomados de n en n es igual a variaciones sin repetición de m elementos tomados de n en n dividido por permutaciones de n.
También se pueden calcular las combinaciones aplicando factoriales:
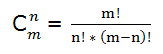
Veamos un ejemplo: con las 5 vocales cuantos grupos de 3 letras podemos formar teniendo en cuenta que ninguna letra se puede repetir y que el orden no importa.
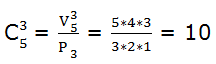
Vamos a calcularlo nuevamente aplicando factoriales:
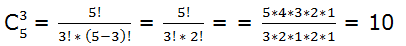
Veamos otros ejemplos:
De una clase de 20 alumnos se seleccionan 3 para que participen en un torneo inter-escolar. ¿Cuántos grupos diferentes podríamos formar?
m = 20 (número de alumnos de la clase)
n = 3 (tamaño del grupo)
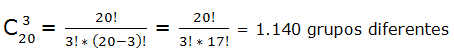
En una final de futbol se seleccionan 5 jugadores de un equipo para el lanzamiento de penaltis. ¿Cuántos grupos se podrían formar?
m = 11 (número de jugadores del equipo)
n = 5 (número de jugadores que van a lanzar los penaltis; no importa el orden)
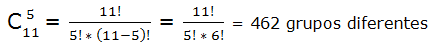
En una carrera de caballos con 12 participantes tienes que elegir los 2 caballos ganadores (no importa el orden de llegada). ¿Cuántos posibles resultados podrían darse?
m = 12 (número de caballos)
n = 2 (número de caballos ganadores)
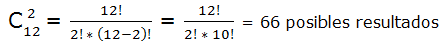
b) Combinaciones con repetición
En las combinaciones con repetición un mismo elemento sí puede estar repetido (una o más veces) dentro del grupo.
En este caso n puede ser > m.
Por ejemplo: con las 5 vocales cuantos grupos de 10 letras puedo formar (la misma vocal podría estar repetida hasta 10 veces).
Un posible grupo sería: “A A A A A A A A A A”
En este ejemplo: m = 5 (nº de vocales) y n = 10 (tamaño del grupo)
Las combinaciones con repetición se representan por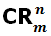 
Para calcular el número de grupos que se pueden formar se aplica la fórmula
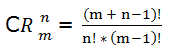
Veamos el ejemplo anterior: con las 5 vocales cuantos grupos de 10 letras podemos formar.
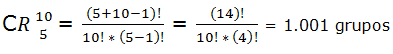
Veamos otros ejemplos:
Lanzamos un dado 7 veces. ¿Cuántos posibles resultados podemos obtener si el orden en el que aparezcan los números no importa?
m = 6 (números del dado)
n = 7 (número de lanzamientos)
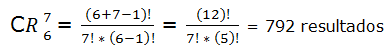
Lanzamos una moneda al aire 10 veces. ¿Cuántos posibles resultados podemos obtener si el orden en el que aparezcan las caras y las cruces no importa?
m = 2 (posibles resultados: cara y cruz)
n = 10 (número de lanzamientos)
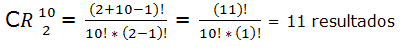
En una clase de 25 alumnos se sortean 3 balones de fútbol iguales; un mismo alumno puede llevarse los 3 premios. ¿Cuántos posibles resultados pueden darse si no importa el orden de consecución de los premios?
m = 25 (nº de alumnos que participan en el sorteo)
n = 3 (número de premios)
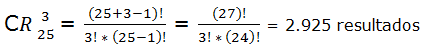
2.- Ejemplos de combinatoria
1.- ¿De cuantas formas se podrían ordenar los 12 meses del año?
Aplicamos permutaciones ya que:
Intervienen todos los elementos
No hay repeticiones
El orden importa
P12 = 12! = 479.001.600
2.- En una pizzería puedes elegir 5 ingredientes para tu pizza (de un total de 15 ingredientes diferentes). ¿Cuántas posibilidades tienes?
Aplicamos combinaciones ya que:
El orden no importa (da igual poner primero el queso y luego el jamón que viceversa)
Si se pueden repetir los ingredientes aplicamos combinaciones con repetición:
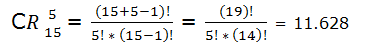
Si no se pueden repetir los ingredientes aplicamos combinaciones sin repetición:
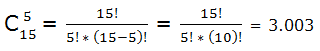
3.- Apuestas con tu amigo los 5 equipos que van a quedar primeros en la liga (donde participan 20 equipos) con el orden correspondiente.
Aplicamos variaciones sin repetición ya que:
No hay repeticiones (un mismo equipo no puede ocupar 2 puestos diferentes)
El orden importa
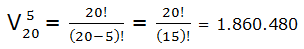
4.- Lanzamos los dados 7 veces; ¿Cuántos resultados diferentes podemos obtener?
Si el orden sí nos importa (consideramos que el resultados “1 – 1 – 1 – 1- 1- 1 -2” es distinto del “2 – 1 – 1 – 1- 1- 1 -1”) aplicamos variaciones con repetición (un mismo número puede salir hasta 7 veces).
m = 6 (el dado tiene 6 números)
n = 7 (hacemos 7 lanzamientos)
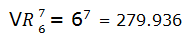
Si el orden no nos importa (consideramos que el resultados “1 – 1 – 1 – 1- 1- 1 -2” es igual que el “2 – 1 – 1 – 1- 1- 1 -1”) aplicamos combinaciones con repetición.
