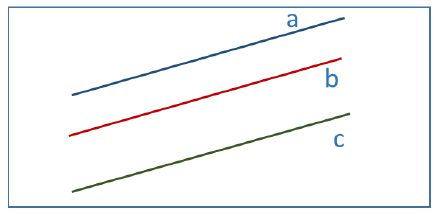
Sistema de tres ecuaciones con dos incógnitas
Para su solución se aplica el método de Gauss.
Para ello se representa el sistema de forma matricial y se analiza su matriz ampliada (aquella en la que se representan los coeficientes y los términos independientes). Esta matriz tendrá 3 filas y 3 columnas.
Partiendo de una matriz ampliada genérica:
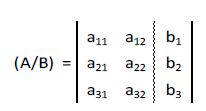
El método de Gauss consiste en realizar transformaciones elementales en las filas de la matriz hasta obtener una matriz con la siguiente forma:
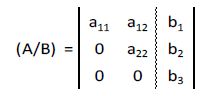
Esta matriz recibe el nombre de matriz ampliada escalonada.
Las operaciones que se pueden realizar son:
a) Multiplicar (dividir) una fila por un número real distinto de cero
b) Sumar (restar) a una fila otra fila multiplicada por un número real distinto de cero
c) Intercambiar el lugar de dos filas entre sí.
Realizando estas operaciones obtenemos un sistema equivalente al sistema inicial.
Para eliminar los coeficientes a21 , a31 y a32 hay que proceder precisamente en este orden. Los dos primeros elementos se eliminan operando con la fila 1ª y el tercer elemento operando con la fila 2ª.
Una vez obtenida la matriz ampliada escalonada se pueden dar los siguientes casos:
a) a22 ≠ 0. En este supuesto se pueden presentar dos variantes:
a.1) b3 ≠ 0. Sistema incompatible
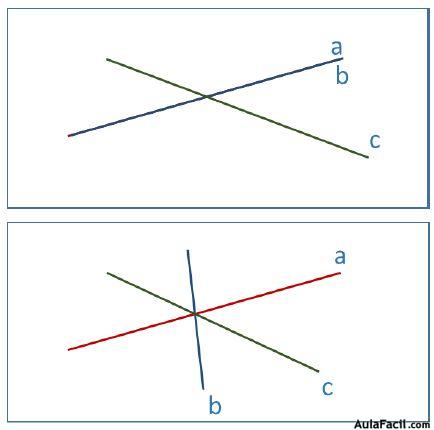
Representaría bien 2 rectas paralelas y otra que las corta, bien tres rectas que se cortan 2 a 2.
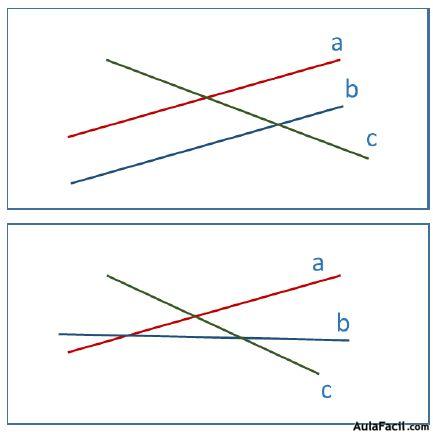
a.2) b3 = 0. Una de las ecuaciones sería 0 = 0 por lo que no afecta a la resolución del problema. El sistema quedaría reducido a un sistema de dos ecuaciones con solución única.
Representaría bien 2 rectas coincidentes y otra que las corta, bien tres rectas que se cortan en el mismo punto.
b) a22 = 0. En este supuesto se pueden presentar tres variantes:
b.1) Si b2 = b3 = 0 entonces quedarían dos ecuaciones de la forma 0 = 0 que no afectan a la resolución del problema. El sistema quedaría con una única ecuación con dos incógnitas y tendría infinitas soluciones.
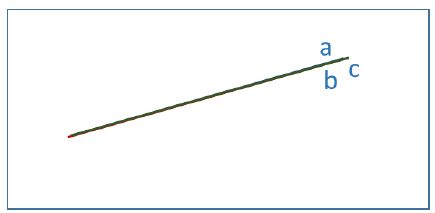
Representaría 3 rectas coincidentes.
b.2) Si b2 ≠ 0 y b3 = 0 (o b2 = 0 y b3 ≠ 0) una ecuación tendría la forma 0 = 0 y otra la forma 0 = k situación esta última imposible por lo que el sistema es incompatible.
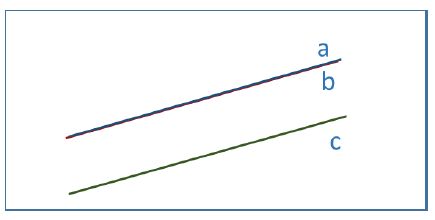
Representaría bien 2 rectas paralelas y la otra las corta, bien 2 rectas coincidentes y la otra paralela.
b.3) Si b2 ≠ 0 y b3 ≠ 0 habría dos ecuaciones con la forma 0 = K lo que es imposible. Sería por tanto un sistema incompatible.
Representaría bien 3 rectas paralelas, bien 2 rectas coincidentes y la otra paralela.