Ejercicios
Veamos algunos ejemplos:
1er ejemplo
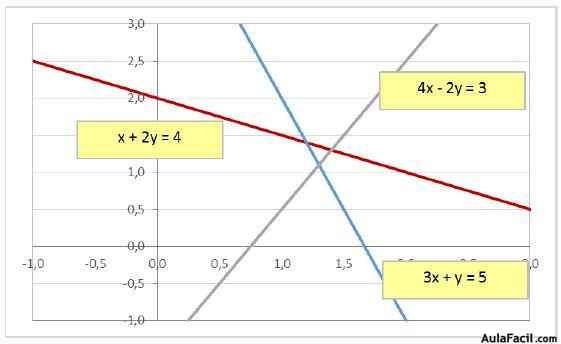
x + 2y = 4
3x + y = 5
4x – 2y = 3
Representamos su matriz ampliada. Hay que vigilar que las diferentes incógnitas y los términos
independientes están en las columnas correspondientes:
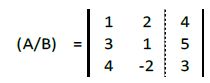
A la segunda fila le restamos la primera multiplicada por 3:
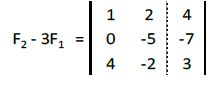
A la tercera fila le restamos la primera multiplicada por 4:
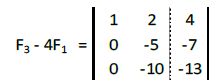
A la tercera fila le restamos la segunda multiplicada por 2:
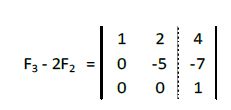
De los posibles casos vistos anteriormente nos encontraríamos en el a.1. (a22 ≠ 0 y b3 ≠ 0) Es por tanto un sistema incompatible.
Vamos a resolver el sistema anterior:
La matriz a la que hemos llegado representa el siguiente sistema de ecuaciones, equivalente con el sistema inicial:
x + 2y = 4
-5y = -7
0 = 1
Vemos que la tercera ecuación de este sistema es imposible, por lo que este sistema no tiene solución.
2º ejemplo
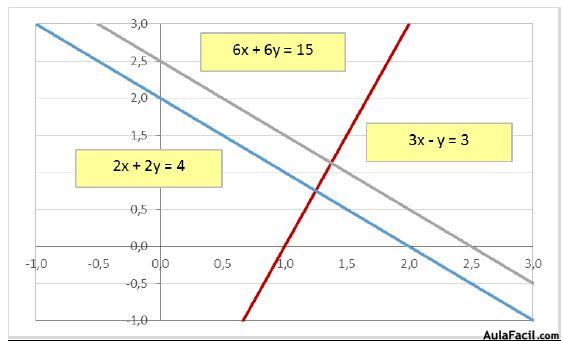
3x - y = 3
2x + 2y = 4
6x + 6y = 15
Representamos su matriz ampliada:
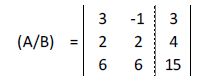
Multiplicamos la primera fila por 2 y la segunda por 3:
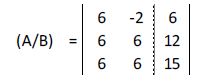
A la segunda fila le restamos la primera:

A la tercera fila le restamos la primera:
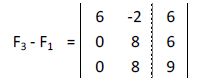
A la tercera fila le restamos la segunda:
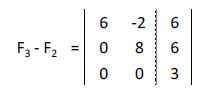
De los posibles casos vistos anteriormente nos encontraríamos nuevamente en el a.1. (a22 ≠ 0 y b3 ≠ 0) Es por tanto un sistema incompatible.
Vamos a resolver el sistema anterior:
La matriz a la que hemos llegado representa el siguiente sistema de ecuaciones, equivalente con el sistema inicial:
6x - 2y = 6
8y = 6
0 = 3
Al igual que en el ejemplo anterior la tercera ecuación de este sistema es imposible, por lo que este sistema no tiene solución.
3er ejemplo
4x + 3y = -2
3x + 4y = 1
12x + 9y = -6
Representamos su matriz ampliada:
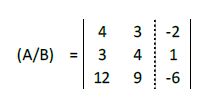
Multiplicamos la primera fila por 3 y la segunda por 4:
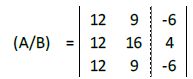
A la segunda fila le restamos la primera:
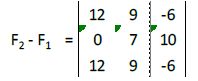
A la tercera fila le restamos la primera:
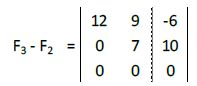
De los posibles casos vistos anteriormente nos encontraríamos en el a.2. (a22 ≠ 0 y b3 = 0). El sistema quedaría reducido a un sistema de dos ecuaciones con solución única.
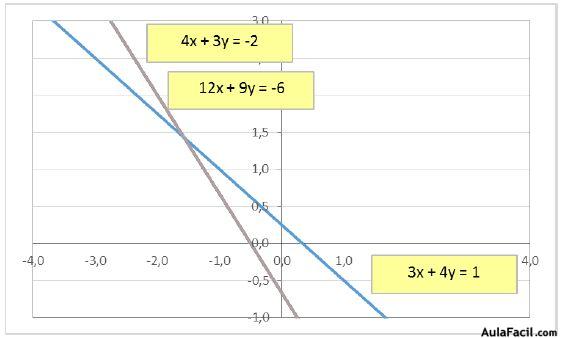
La primera y la tercera ecuación representan rectas superpuestas. La solución de este sistema es el punto de cruce de la primera (o de la tercera ecuación ya que representan la misma recta), con la segunda recta.
Vamos a resolver el sistema anterior:
La matriz a la que hemos llegado representa el siguiente sistema de ecuaciones, equivalente con el sistema inicial:
12x + 9y = -6
7y = 10
En la segunda ecuación despejamos “y”:
y1 = 10 / 7 = 1,4286
En la primera ecuación sustituimos la “y” por su valor:
12x + 9*(1,4286) = -6
12x + 12,8571 = -6
12x = -18,8571
x1 = -18,8571 / 12 = -1,5714
Por lo tanto, las soluciones de este sistema de ecuaciones es:
x1 = -1,5714
y1 = 1,4286
Vamos a comprobar que estas soluciones cumplen las igualdades del sistema inicial de ecuaciones:
1ª ecuación:
4x + 3y = -2
4*(-1,5714) + 3*(1,4286) = -2
-2 = -2
2ª ecuación:
3x + 4y = 1
3*(-1,5714) + 4*(1,4286) = 1
1 = 1
3ª ecuación:
12x + 9y = -6
12*(-1,571) + 9*(1,4286) = -6
-6 = -6
Por lo tanto las soluciones calculadas hacen cumplir la igualdad en las tres ecuaciones del sistema.
4º ejemplo
2x - y = 1
x = 1
y = 1
Representamos su matriz ampliada:
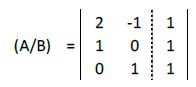
Multiplicamos la segunda fila por 2:
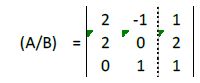
A la segunda fila le restamos la primera:
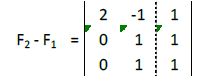
A la tercera fila le restamos la segunda:
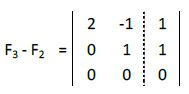
De los posibles casos vistos anteriormente nos encontraríamos en el a.2. (a22 ≠ 0 y b3 = 0). El sistema quedaría reducido a un sistema de dos ecuaciones con solución única.
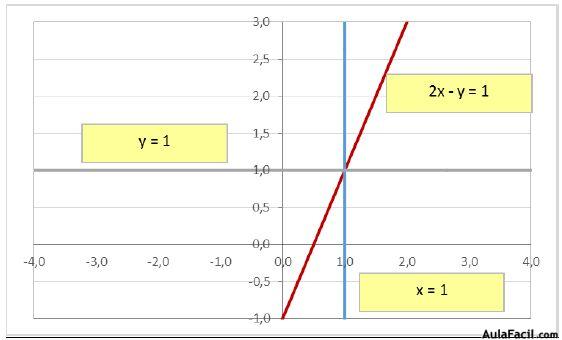
Vamos a resolver el sistema anterior:
La matriz a la que hemos llegado representa el siguiente sistema de ecuaciones, equivalente con el sistema inicial:
2x - y = 1
y1 = 1
Ya conocemos el valor de “y”: en la primera ecuación sustituimos esta incógnita por su valor:
2x - 1 = 1
2x = 2
x1 = 1
Por lo tanto, las soluciones de este sistema de ecuaciones es:
x1 = -1
y1 = 1
Vamos a comprobar que estas soluciones cumplen las igualdades del sistema inicial de ecuaciones:
1ª ecuación:
2x - y = 1
2*1 - 1 = 1
1 = 1
2ª ecuación:
x = 1
1 = 1
3ª ecuación:
y = 1
1 = 1
Por lo tanto las soluciones calculadas hacen cumplir la igualdad en las tres ecuaciones del sistema.
5º ejemplo
3x - 2y = 2
6x - 4y = 4
-3x + 2y = -2
Representamos su matriz ampliada:
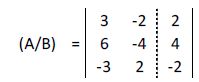
Multiplicamos la primera fila por 2:
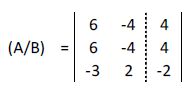
A la segunda fila le restamos la primera:
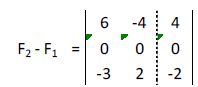
Multiplicamos la tercera fila por 2:
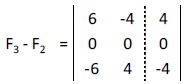
A la tercera fila le sumamos la primera:
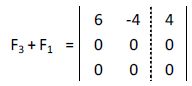
De los posibles casos vistos anteriormente nos encontraríamos en el b.1. (a22 = 0 y b1 = b2 = 0).
El sistema quedaría con una única ecuación con dos incógnitas y tendría infinitas soluciones.
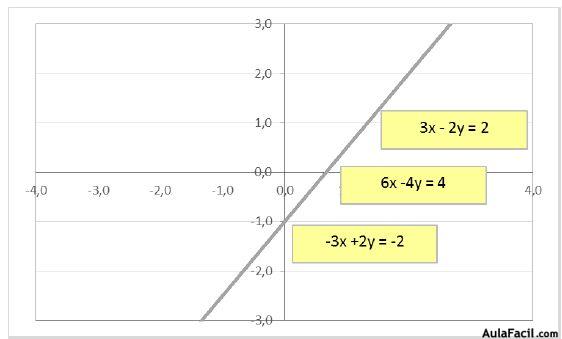
Las tres rectas son coincidentes.
Vamos a resolver el sistema anterior:
La matriz a la que hemos llegado representa el siguiente sistema de ecuaciones, equivalente con el sistema inicial:
6x – 4y = 4
Es una ecuación con 2 incógnitas por lo que tiene infinitas soluciones: en función del valor que tome una de ellas podemos calcular el valor de la otra:
Si x = 1:
6 – 4y = 4
4y = 2
y = 0,5
Si x = 3:
18 – 4y = 4
4y = 14
y = 3,5
Si x = -2:
-12 – 4y = 4
4y = -16
y = -4


