Sistema cuadrado

Cuando un sistema de ecuaciones tiene el mismo número de ecuaciones que de incógnitas decimos que es un sistema cuadrado. La matriz de coeficientes es cuadrada. El sistema se puede escribir matricialmente:

A * X = B

Siendo:

A: la matriz de coeficientes

X: la matriz de incógnitas

B: la matriz de términos independientes

Vamos a tratar de despejar X para ellos es necesario que la matriz A posea inversa A-1. En este caso podemos:

A-1 * A * X = A-1 * B

De esta manera calcularíamos X y el sistema tendría solución única.

Si la matriz A no posee inversa no se puede aplicar este método de resolución.

Para ver si una matriz A tiene inversa calculamos su determinante “det (A)” y este debe ser distinto de cero.

Cálculo del determinante de una matriz

Dada una matriz cuadrada A de tres filas y 3 columnas:

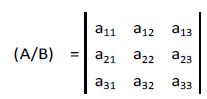
Su determinante se calcula:

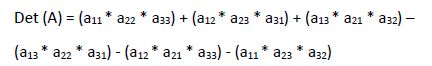
Gráficamente representamos en azul las multiplicaciones que suman y en naranja las multiplicaciones que restan:

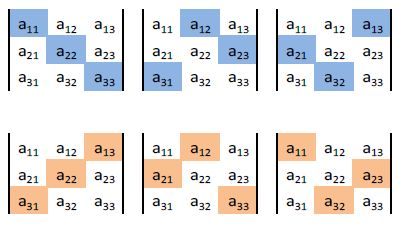
Veamos un ejemplo:

Dado el siguiente sistema lineal de 3 ecuaciones:

x + 2y – 3z = 2

3x - y + z = 1

-2x + 3y + 2z = 3

Se trata de un sistema cuadrado (3 ecuaciones con 3 incógnitas) vamos a ver si se puede resolver:

Representamos la matriz de coeficientes:

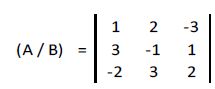
Calculamos su determinante: |A| = -42 ≠ 0

Luego la matriz A tiene matriz inversa 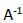. Vamos a calcularla aplicando un procedimiento que se denomina “cálculo por determinantes”:

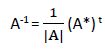
Siendo:

|A|: Determinante de la matriz

A*: Matriz adjunta.

(A*) t: Traspuesta de la matriz adjunta

Comenzamos a calcular:

|A| = - 42

A*: Para calcular la matriz adjunta se sustituye cada elemento de la matriz por su determinante:

En el cuadro siguiente subrayamos en naranja el elemento de la matriz que vamos a sustituir por sus determinante y en azul los elementos de la matriz que forman parte de sus determinantes.

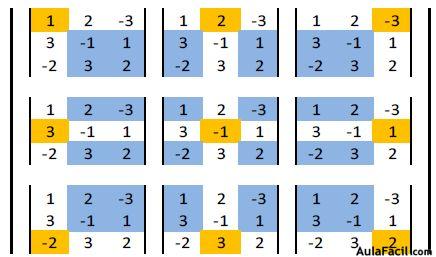
Cada determinante se calcula de la siguiente manera (vamos a calcular el del primer elemento):

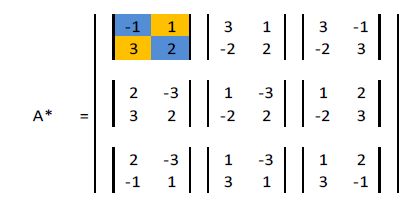
Multiplicamos en cruz: con fondo azul suma y con fondo naranja resta: El determinante de a11 = (-1 * 2) – (1 * 3) = -5

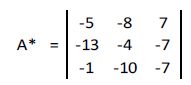
La traspuesta de la matriz adjunta se calcula sustituyendo las filas por columnas:

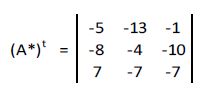
Luego la matriz inversa es igual:

Vimos que: X = 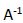 * B

Luego:

Una vez calculadas las soluciones, habría que ir al sistema inicial, sustituir las incógnitas por sus soluciones y verificar que se cumplen las igualdades:

x + 2y – 3z = 2

3x - y + z = 1

-2x + 3y + 2z = 3

Sustituyendo:

(0,6190) + 2*(1.1905) – 3*(0,3333) = 2

3*(0,6190) - (1.1905) + (0,3333) = 1

-2*(0,6190) + 3*(1.1905) + 2*(0,3333) = 3

Operando:

2 = 2

1 = 1

3 = 3