Regla de Cramer
Cuando el sistema es cuadrado (mismo número de ecuaciones que de incógnitas) y la matriz tiene inversa, se denomina sistema de Cramer.
Este sistema se puede resolver aplicando un método que se denomina Regla de Cramer:
La solución de una incógnita cualquiera del sistema “x j" se calcula dividiendo:
El determinante que resultaría de sustituir en la matriz la columna que ocupa dicha incógnita por la columna de los términos independientes.
Entre:
El determinante de la matriz inicial.
Esta regla nos permite calcular de forma sencilla las soluciones del sistema:
1er ejemplo
x + 2y – 3z = 2
3x - y + z = 1
-2x + 3y + 2z = 3
Cumple las dos condiciones para aplicar la Regla de Cramer: es un sistema cuadrado y la matriz tiene inversa.
Vimos que la matriz de coeficientes era:
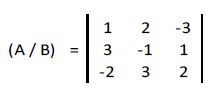
Y que su determinante era -42
a) Vamos a calcular la solución de la incógnita “x”: sustituimos en la matriz la columna de los coeficientes de x por la columna de los términos independientes:
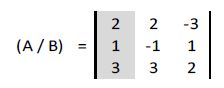
Calculamos su determinante: |A| = -26
Luego x = -26 / -42 = 0,6190
b) Solución de la incógnita “y”: sustituimos en la matriz la columna de los coeficientes de x por la columna de los términos independientes:
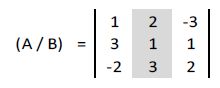
Calculamos su determinante: |A| = -50
Luego y = -50 / -42 = 1,1905
c) Solución de la incógnita “z”: sustituimos en la matriz la columna de los coeficientes de x por la columna de los términos independientes:
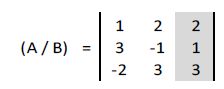
Calculamos su determinante: |A| = -14
Luego z = -14 / -42 = -0,333
Podemos ver que las soluciones calculadas por este método son iguales a las obtenidas en el apartado anterior.
2º ejemplo
3x - y + 4z = 1
2x + 3y + 2z = 5
x + y + 3z = 2
Es un sistema cuadrado. Comprobamos si la matriz tiene inversa. Para ver si una matriz A tiene inversa calculamos su determinante “det(A)” y este debe ser distinto de cero.
La matriz de coeficiente es:
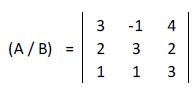
Y que su determinante era 21
a) Vamos a calcular la solución de la incógnita x: sustituimos en la matriz la columna de los coeficientes de x por la columna de los términos independientes:
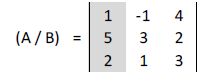
Calculamos su determinante: |A| = 14
Luego x1 = 14 / 21 = 0,6666
b) Solución de la incógnita y: sustituimos en la matriz la columna de los coeficientes de x por la columna de los términos independientes:
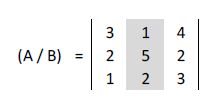
Calculamos su determinante: |A| = 25
Luego y1 = 25 / 21 = 1,1905
c) Solución de la incógnita z: sustituimos en la matriz la columna de los coeficientes de x por la columna de los términos independientes:
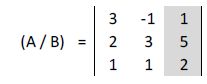
Calculamos su determinante: |A| = 1
Luego z1 = 1 / 21 = 0,0476
Ya tenemos la solución:
x1 = 0,6666
y1 = 1,1905
z1 = 0,0476
Vamos a verificar que estos valores hacen cumplir las igualdades del sistema inicial:
3x - y + 4z = 1
2x + 3y + 2z = 5
x + y + 3z = 2
Sustituyendo:
3*(0,6666) - (1,1905) + 4*(0,0476) = 1
2*(0,6666) + 3*(1,1905) + 2*(0,0476) = 5
(0,6666) + (1,1905) + 3*(0,0476) = 2
Operando:
1 = 1
5 = 5
2 = 2
Teorema de Rouché–Frobenius
Este teorema nos permite saber sin un sistema cualquiera de ecuaciones lineales tiene solución, y si la solución es única o son infinitas. Este sistema no permite calcular las soluciones, únicamente nos indica si hay o no.
Para ello calculamos el rango de la matriz A y de la matriz ampliada (A / B). Puede ocurrir:
a) Rg (A) = Rg (A / B). La matriz tiene solución.
Si el Rg (A) = nº de incógnitas entonces la solución es única (sistema compatible determinado)
Si el Rg (A) < nº de incógnitas entonces hay infinitas soluciones (sistema compatible indeterminado)
b) Rg (A) ≠ Rg (A / B). La matriz no tiene solución (sistema incompatible)
Sistemas homogéneos
Sistema homogéneo es aquel que tiene todos los términos independientes nulos.
x + 2y – 3z = 0
3x - y + z = 0
-2x + 3y + 2z = 0
Todos sistema homogéneo es compatible (tiene solución) ya que cuando todas las incógnitas toman el valor 0 se cumplen las ecuaciones (esta solución se denomina solución trivial). La cuestión es determinar si es un sistema compatible determinado (con 1 sola solución) o compatible indeterminado (con infinitas soluciones).
Aplicando el teorema de Rouche que vimos anteriormente se pueden plantear dos situaciones:
Si el Rg (A) = nº de incógnitas entonces la solución es única, la solución trivial (sistema compatible determinado)
Si el Rg (A) < nº de incógnitas entonces hay infinitas soluciones (sistema compatible indeterminado).
Analicemos el ejemplo anterior:
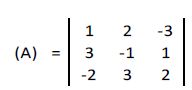
a) El rango de la matriz será >= 1 ya que hay elementos dentro de la matriz distintos de 0.
b) El rango de la matriz también será >= 2 ya que existe alguna submatriz cuadrada de orden 2 cuyo determinante no es nulo.
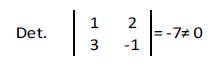
c) Por último vamos a comprobar si el rango de la matriz = 3.

Luego efectivamente el rango de la matriz es 3. Por lo tanto Rg (A) = 3 = nº de incógnitas, por lo que la solución es única (la solución trivial)


