Ejercicios
Veamos algunos ejemplos:
1er ejemplo
x + 2y – 3z = 2
3x - y + z = 1
-2x + 3y + 2z = 3
Representamos su matriz ampliada:
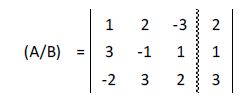
A la segunda fila le restamos la primera multiplicada por 3:
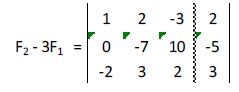
A la tercera fila le sumamos la primera multiplicada por 2:
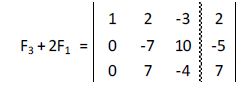
A la tercera fila le sumamos la segunda:
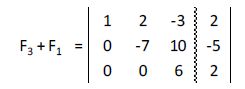
De esta manera hemos obtenido la matriz ampliada escalonada:
De los posibles casos vistos anteriormente nos encontraríamos en el modelo a) (sistema escalonado).
Esta última matriz representa un sistema de 3 ecuaciones equivalente al inicial compuesto por:
x + 2y – 3z = 2
-7y + 10z = -5
6z = 2
a) Comenzamos por despejar “z” en la tercera ecuación:
6z = 2
z1 = 2 / 6 = 0,3333
b) En la segunda ecuación despejamos “y”:
-7y + 10z = -5
y1 = (-5 – 10z) / (-7) = (-5 – 10*0,3333) / (-7) = 1,1905
c) En la primera ecuación despejamos “x”:
x + 2y – 3z = 2
x1 = 2 - 2y + 3z = 2 – 2*1,1905 + 3*0,3333 = 0,6190
Por lo tanto la solución a este sistema de 3 ecuaciones sería (x1 = 0,6190; y1 = 1,1905; z1 = 0,3333) y representa el punto en el plano en el que se cortan estos 3 planos.
Por último vamos a chequear en el sistema de ecuaciones que esta solución hace cumplir simultáneamente las 3 igualdades)
x + 2y – 3z = 2
3x - y + z = 1
-2x + 3y + 2z = 3
1ª ecuación:
x + 2y – 3z = 2
0,6190 + 2*1,1905 – 3*0,3333 = 2
2 = 2
2ª ecuación:
3x - y + z = 1
3*0,6190 - 1,1905 + 0,3333 = 1
1 = 1
3ª ecuación:
-2x + 3y + 2z = 3
-2*0,6190 + 3*1,1905 + 2*0,3333 = 3
3 = 3
2º ejemplo
5x + 4y + 2z = 5
-x - 2y + z = -2
x + y + 2z = 1
Representamos su matriz ampliada:
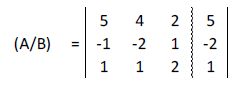
Multiplicamos la segunda fila por 5 y le sumamos la primera:

Multiplicamos la tercera fila por 5 y le restamos la primera:
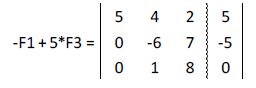
Multiplicamos la tercera fila por 6 y le sumamos la segunda:
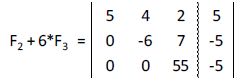
De esta manera hemos obtenido la matriz ampliada escalonada:
De los posibles casos vistos anteriormente nos encontraríamos en el modelo a) (sistema escalonado).
Esta última matriz representa un sistema de 3 ecuaciones equivalente al inicial compuesto por:
5x + 4y + 2z = 5
-6y + 7z = -5
55z = -5
a) Comenzamos por despejar “z” en la tercera ecuación:
55z = -5
z1 = -5 / 55 = -0,0909
b) En la segunda ecuación despejamos “y”:
-6y + 7z = -5
y1 = (-5 - 7z) / (-6) = (-5 – 7*(-0,0909)) / (-6) = 0,7272
c) En la primera ecuación despejamos “x”:
5x + 4y + 2z = 5
x1 = (5 - 4y - 2z) / 5 = (5 – 4*(0,7272) – 2*(-0,0909)) / 5 = 0,4545
Por lo tanto la solución a este sistema de 3 ecuaciones sería (x1 = 0,4545; y1 = 0,7272; z1 = -0,0909) y representa el punto en el plano en el que se cortan estos 3 planos.
Por último vamos a chequear en el sistema de ecuaciones que esta solución hace cumplir simultáneamente las 3 igualdades)
5x + 4y + 2z = 5
-x - 2y + z = -2
x + y + 2z = 1
1ª ecuación:
5x + 4y + 2z = 5
(5*0,4545) + (4*0,7272) + (2*(-0,0909)) = 5
5 = 5
2ª ecuación:
-x - 2y + z = -2
-0,4545 - (2*0,7272) - 0,0909 = -2
-2 = -2
3ª ecuación:
x + y + 2z = 1
0,4545 + 0,7272 + (2*(-0,0909)) = 1
1 = 1
3er ejemplo
2x + 4z = 3
3x + y + 2z = 1
6x + 2y + 4z = 7
Representamos su matriz ampliada: Como la primera ecuación no lleva incógnita “y”, en la columna de la matriz correspondiente a esta incógnita hemos puesto 0.
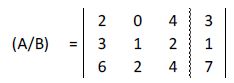
Multiplicamos la primera fila por 3 y la segunda por 2:

A la segunda fila le restamos la primera:

A la tercera fila le restamos la primera:
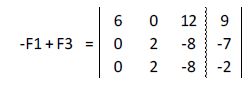
A la tercera fila le restamos la segunda:
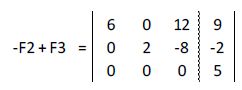
De esta manera hemos obtenido la matriz ampliada escalonada:
De los posibles casos vistos anteriormente nos encontraríamos en el modelo c) (sistema incompatible).
Esta última matriz representa un sistema de 3 ecuaciones equivalente al inicial compuesto por:
6x + 12z = 9
2y - 8z = -2
0 = 5
Esta última ecuación no es posible; el sistema no tiene solución.
4º Ejemplo
x - 3y + 2z = 5
2x - y + 3z = 2
2x - 6y + 4z = 10
Representamos su matriz ampliada:
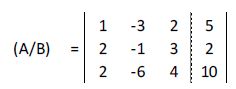
Multiplicamos la primera fila por 2
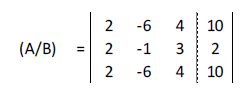
A la segunda fila le restamos la primera:
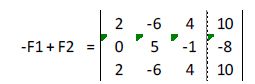
A la tercera fila le restamos la primera:
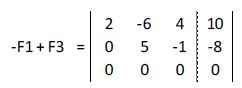
De esta manera hemos obtenido la matriz ampliada escalonada:
De los posibles casos vistos anteriormente nos encontraríamos en el modelo b): Es un sistema compatible indeterminado (El sistema tiene infinitas soluciones: hay que despejar una o más incógnitas en función de otras).
Esta última matriz representa un sistema de 2 ecuaciones equivalente al inicial compuesto por:
2x - 6y + 4z = 10
5y - z = -8
En la segunda ecuación despejamos la incógnita “z”:
z = 5y + 8
En la primera ecuación sustituimos la incógnita “z” por esta expresión:
2x - 6y + 4*(5y + 8) = 10
2x - 6y + 20y + 32 = 10
2x + 14y = -22
Tenemos una ecuación con 2 incógnitas por lo que tiene infinitas soluciones: en función del valor que toma una de las incógnitas podemos calcular el valor de las otras dos:
Si x = 1:
2 + 14y = -22
14y = -24
y = -24 / 14 = -1,7142
z = 5*(-1,7142) + 8 = -0,5714
Si x = 4:
8 + 14y = -22
14y = -30
y = -30 / 14 = -2,1429
z = 5*(-2,1429) + 8 = -2,7143
Si x = -3:
-6 + 14y = -22
14y = -16
y = -16 / 14 = -1,1429
z = 5*(-1,1429) + 8 = 2,2857


